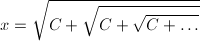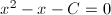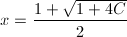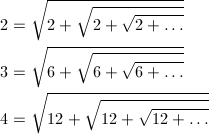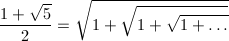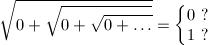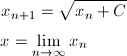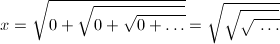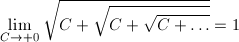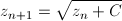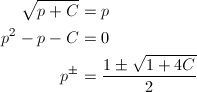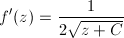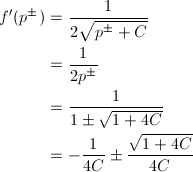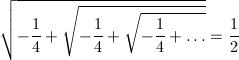根号(ルート)の中にまた根号があることを多重根号(nested radical)と言います。例えば、こんな感じです。
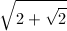
さて、ここで、根号の中に根号を無限に連ねていくとどうなるでしょう。
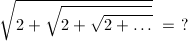
このような形を無限多重根号(infinite nested radical)と呼びます。実はこれは答えを出すことができます。
まずは、上式をxとおき、両辺を2乗します。
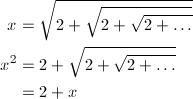 … (式1)
… (式1)
すると、根号を外した右辺にはx自身が現れるため、簡単な二次方程式になりました。これを解くと、xは2または-1となりますが、根号は正の平方根を表すものですから、-1は不適当で、答えは2と求められました。
先ほどの問題では、根号(ルート)の中身が全て2でしたが、これを任意の正の実数の場合へ一般化してみます。
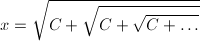 … (式2)
… (式2)
手順は先ほどと全く同じで、次の二次方程式を得ます。
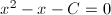 … (式3)
… (式3)
二次方程式の解の公式より、
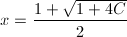 … (式4)
… (式4)
となります。なお、C > 0では√{1 + 4C} > 1となるため、xが正となるために分子の符号は+を選びました。C = 2を代入すると、先ほどの計算通り2となります。他にも、C = 6で3、C = 12で4などが得られます。
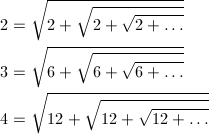
C = 1の場合は、黄金比となります。さすが、最も美しい比なだけあって、このような美しい表記も持っているわけですね。
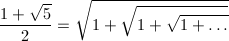
ところで、先ほどは根号の中の定数Cを正の実数に限定しましたが、それ以外では成り立たないのでしょうか。例えばC = 0の場合はどうなるでしょう。先ほどと同じ方法でC = 0の場合を考えると、x^2 - x = 0となり、xは0と1の二つが答えになってしまいます。どちらが正しい答えなのでしょうか。それとも、両方とも答えではないのでしょうか。
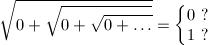
そこで、無限多重根号がそもそもどんなものなのか改めて考えてみます。
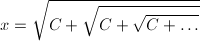
根号の内側から外側に向かって考えると、「Cを足してルートを取る」という作業が無限にくり返し行われているものと見なすことができます。つまり漸化式を使って表すと、
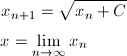 … (式5)
… (式5)
ということです。無限多重根号の値xは、この数列x_nにおいてn → ∞としたときの極限値と考えられます。
ところで、この数列の初項x_0は一体何でしょうか?初項を知るには、無限多重根号を無限の奥底までたどらないといけません。つまり、初項は無いのです。言い換えると、初項が何であっても、同じ極限値xに至らなければ、この無限多重根号は成り立たないと言えます。
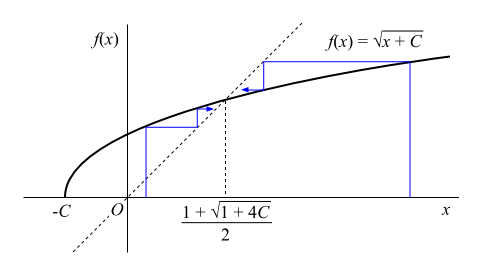
図1-正の実数から始めて収束に至るようす
Cが正の実数の場合、初項によらず必ず先ほど公式で示したただ一つの値に収束します。初項が正の実数の場合は、図1より明らかです。初項が他の複素数であったとしても、「根号を取る」ことと「正の実数を足す」ことはいずれも偏角を0、すなわち正の実数に近づけていくわけですから、結局実軸上の同じ値に収束します。
一方、Cが0の場合は、単に根号を取る作業を無限にくり返すことになります。電卓で適当な数を入れて√ボタンを連打すると分かりますが、たいていの場合これは1に収束します。電卓ではできませんが、負の実数や複素数から始めた場合も、Cが正の実数の場合と同じ理由で、必ず1に収束します。しかし、ただ一つ1には収束しない点があります。それは0です。0から始めると、√ボタンをいくら押しても、0からは全く変化せずずっと0のままです。当然といえば当然です。
つまり、Cが0の場合、初項によって、極限値が0と1の2通りあることになります。二次方程式による解法で0と1が出てきたのはこういうことだったのです。しかし、くり返しますが、数列の初項は無限の彼方にあるため、恣意的にどちらと選択することができません。したがって、C = 0の場合の無限多重根号
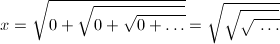
は値を定義できず、数式として意味をなさないことになります。
しかし、Cが0では成り立たないことは分かりましたが、Cを正の方から0に近づけていくと、xが1に近づいていくことは事実です。
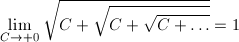
このような表現であれば、問題なさそうです。
先ほど数列として考えた場合の漸化式に着目してみます。
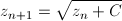 … (式6)
… (式6)
ここからは、複素数の範囲で考えるものとして、文字をzに変えました。これは、複素関数f(z) = √{z + C}による複素力学系をなしていると考えることができます。そこで、複素力学系の考え方を使って、この数列の挙動を調べてみます。
まずは、固定点です。固定点の定義より、
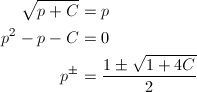 … (式7)
… (式7)
が得られます。簡単のため、まずCを実数に限定すると、Cの値によって固定点pは次のようになります。pの実部が必ず正になることに注意して下さい。
表1-複素力学系f(z) = √{z + C}の固定点
| 範囲 | 固定点 |
|---|
| 0 < C |
実数の範囲にp^{+}が一つ存在 |
| -1/4 < C ≤ 0 |
実数の範囲にp^{+}とp^{-}が存在 |
| C = -1/4 |
p^{+} = p^{-} = 1/2 |
| C < -1/4 |
実部が1/2の複素数の範囲にp^{+}とp^{-}が存在 |
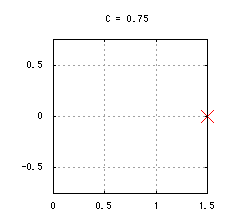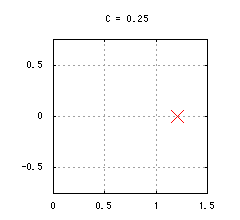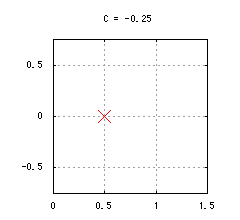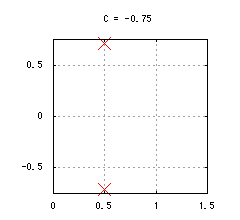
図2-複素力学系
f(z) = √{z + C}の固定点
次にこれらの固定点の性質を調べます。まず、微分係数f'(z)を求めると、
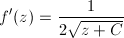 … (式8)
… (式8)
なので、
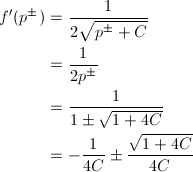 … (式9)
… (式9)
となり、Cによって次のようになります。
表2-複素力学系f(z) = √{z + C}の各固定点の性質
| 範囲 |
|f'(p^{+})| |
|f'(p^{-})| |
| C < 0 |
< 1 (吸引的) |
なし |
| -1/4 < C ≤ 0 |
< 1 (吸引的) |
> 1 (反発的) |
| C = -1/4 |
= 1 (中立的) |
| C < -1/4 |
< 1 (吸引的) |
< 1 (吸引的) |
先ほど、C = 0の場合について考察しましたが、-1/4 < C ≤ 0の範囲では固定点が2つ存在するため、初期値によって収束先が変わってしまい無限多重根号の値が定義できないことが改めて分かります。同様にC < -1/4の範囲でも、固定点は2つ存在し、無限多重根号の値としては定義ができません。
しかし、C = -1/4の場合は固定点はただ一つです。しかし、この固定点は中立的であるため、周囲の点を引き寄せるかどうかは微分係数の値からは分かりません。もし、複素平面全体の点をこの固定点が吸引するとすれば、
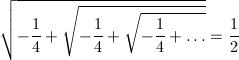
が成り立つと言えることになります。
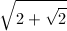
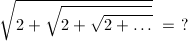
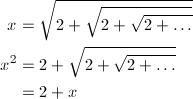 … (式1)
… (式1)