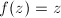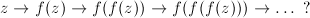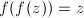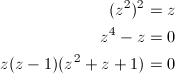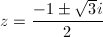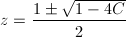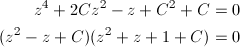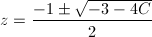複素力学系入門
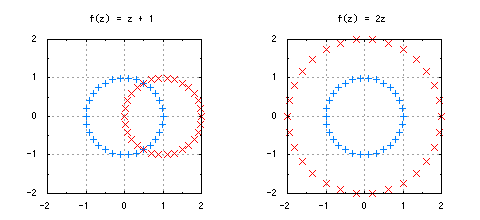
図1-複素関数による複素平面上での点の移動
複素数zを変数とする関数f(z)を考えます。複素数は、複素平面上の一点として表されます。f(z)が返す値もまた複素数ですから、同じく複素平面上のどこかの一点で表されます。このとき、複素平面上の点zは、関数fが作用したことによって別の点f(z)に移った、と考えることができます。このように、複素数が関数によって複素平面上をどのように動くかを考えたものが、複素力学系(complex dynamics)です。
例えば、f(z) = z + 1を考えます。この関数は、与えられた複素数zに1を加えます。この関数によって、複素平面上のあらゆる点は、右方向にずらされることが想像できます。f(z) = 2zではどうでしょうか。与えられた複素数zの絶対値を2倍にするわけですから、複素平面上のあらゆる点は、原点から2倍の距離に遠ざかることになります。図1に点の移動のようすを示しました。青色の単位円が、それぞれの関数によって、赤色の位置・大きさに変化しています。このように、“複素平面上での点の動き”に着目します。
関数によって、複素平面上の全ての点が移動するとは限りません。中には、関数によって同じ値となる点もありえます。そのような点は、固定点または不動点と呼ばれます。固定点は、定義より次の式を満たします。
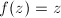 … (式1)
… (式1)
先の例での固定点を考えてみます。f(z) = z + 1の場合は、z + 1 = zとなり、これを満たすzは存在しません。したがって、固定点は存在しません。一方、f(z) = 2zの場合は、2z = zとなり、z = 0が唯一の固定点となります。
複素力学系では、同じ関数fをくり返し何度も作用させたときにどうなるかがしばしば注目されます。
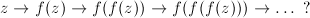 … (式2)
… (式2)
ここで、f(z) = z^2の場合を考えてみましょう。まず、固定点は、z^2 = zより、z = 0と1です。この2つの点に関しては、何度関数を作用させようとも移動しません。
|z| > 1のようなzの場合、2乗をくり返すことで、絶対値がどんどん増大し、無限大に発散してしまいます。一方、|z| < 1となるzでは、絶対値がどんどん小さくなり、0に収束してしまいます。
|z| = 1の場合はどうでしょうか。z = 1の場合は固定点で動きませんが、それ以外の偏角が0でない値θを持つzの場合は、|z| = 1の円周上をぐるぐる回り続けることになります。その中で、θの2^n倍が2πの整数倍に一致するものは、2乗をくり返すうちにいつかz = 1と一致して動かなくなるでしょう。また、θと2πの比がそれ以外の有理数のものは、円周上をぐるぐる回るうちにいつかは元の点(最初の点とは限らない)に戻ってきて周期的な動きとなりますが、比が無理数の場合は、永遠に同じ点には戻らず不規則な動きが続きます。
いろいろな場合が出てきました。まとめると、次のようになります。
表1-複素力学系f(z) = z^2における様々な挙動
| 挙動 | zの条件 | 分類 |
|---|
| 変化しない(固定点) |
z = 0, 1 |
収束/振動 |
| 無限大に発散する |
|z| > 1 |
発散 |
| ある一点に向かって収束する |
|z| < 1, z ≠ 0 |
収束 |
| 途中で固定点に一致して動かなくなる |
|z| = 1, z ≠ 1, θの2^n倍が2πの整数倍 ※ |
| 一定の周期で元の点に戻る |
|z| = 1, z ≠ 1, θと2πの比が有理数(※を除く) |
振動 |
| 上記のどれでもない |
|z| = 1, z ≠ 1, θと2πの比が無理数 |
カオス |
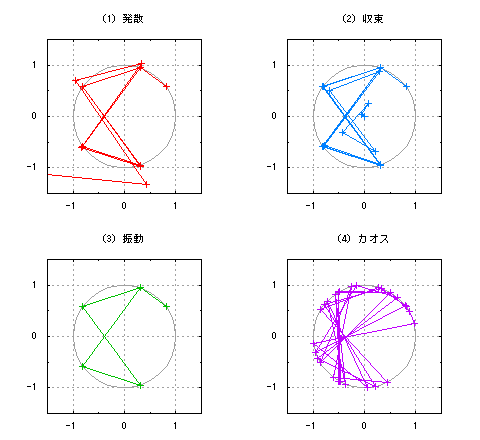
図2-反復計算によるいろいろな挙動
図2は、最初はほぼ同じ位置にあった点が、4つの全く違う動きになる例です。(1)は、z = 1.00001(cos(π/5) + isin(π/5))から始めた場合で、絶対値がわずかに1より大きいために途中で発散し、遠方へ飛んでいってしまっています。(2)は、z = 0.99999(cos(π/5) + isin(π/5))から始めた場合で、こちらは逆に絶対値がわずかに1より小さいために、中心の0へ収束しています。(3)は、z = cos(π/5) + isin(π/5)から始めた場合で、絶対値がちょうど1であるため、半径1の単位円周上で周期的に同じ経路を動き続けています。(4)は、z = cos(π/√{26}) + isin(π/√{26})から始めた場合で、角度の比をわずかに異なる無理数にしたため、発散でも収束でも周期的な動きでもない、全く規則のない動きになっています。
このように、同じ関数を何度も作用させると、複素平面上の点は上記のように様々な動きを示します。どんな関数でもこの全てを見られるとは限りません。f(z) = z^2は、たまたまこのように様々な動きが見られる良い例だったのです。
変化しない点のことを固定点と呼ぶことはすでに説明しましたが、これは周期が1で元の点に戻る点と考えることができ、つまり周期的に元に戻る点(周期点)の仲間とも考えられます。例えば、関数を2回作用させて初めて元に戻る点は2-周期点と呼びます。2-周期点は以下の式を満たします。
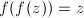 … (式3)
… (式3)
f(z) = z^2について、この式を解いてみます。
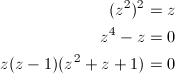 … (式4)
… (式4)
z = 0, 1も解になりますが、これらは固定点(すなわち1-周期点)なので除外すると、z^2 + z + 1 = 0の2つの解、
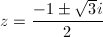 … (式5)
… (式5)
が2-周期点となります。固定点の1を含めると、単位円周上で正三角形をなす3点であることが分かります。
挙動の「上記のどれでもない」場合というのは想像しにくいですが、発散も収束もせず、同じ点を二度踏んだりすることもない、ということです。つまり、有限の範囲を不規則にうろうろとさまよい続けるといった感じでしょうか。この状態は、規則性を見出したり、将来の位置を予想したりすることが難しい場合が多く、カオスと呼ばれます。
固定点は、その近傍の様子によってさらに分類することができます。
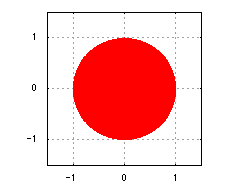
図3-吸引的固定点
z = 0の引力圏
f(z) = z^2の固定点z = 0では、その周囲の点は、全てこの固定点に向かって収束してきていました。この固定点は、周囲の点を引き寄せていると考えることができ、このような点を吸引的固定点と呼びます。一方、もう一つの固定点z = 1では、|z| < 1の点はz = 0へ、|z| > 1の点は無限大へ向かって移動していくわけですから、周囲の点はどんどんz = 1から離れていっていると考えることができます。このような点を反発的固定点と呼びます。
吸引的固定点は、周りの点を引き寄せるという意味で、アトラクタとも呼ばれます。z = 0では、その周囲の|z| < 1となる範囲内の全ての点がz = 0に引き寄せられていました。この範囲のことを、このアトラクタの引力圏または流域と呼びます。
吸引的・反発的の考え方は、周期点にも適用できます。ある周期点の周囲の一定の範囲内の全ての点が、その周期点を通る振動状態に収束するならば、その周期点はアトラクタとなり、その範囲はアトラクタの引力圏です。
固定点が吸引的であるかどうかは、数学的にはその点での関数の微分係数と関連があります。固定点pにおける、微分係数f'(p)の絶対値によって、次のように分類されます。
表2-微分係数と固定点の分類
| 微分係数f'(p)の絶対値 |
分類 |
| |f'(p)| < 1 |
固定点pは吸引的 |
| |f'(p)| > 1 |
固定点pは反発的 |
| |f'(p)| = 1 |
固定点pは中立的 |
微分係数f'(z)とは、おおざっぱに言えば、zの近傍の微小な変位dzがどのように変化するかを表すものです。f'(z)の絶対値が1未満の場合、近傍の微小な変位dzの絶対値は、fの作用によって小さくなることになり、すなわちzにより近づくということです。
f(z) = z^2の微分係数は、f'(z) = 2zです。|f'(0)| = |0| < 1なのでz = 0は吸引的固定点、|f'(1)| = |2| > 1なのでz = 1は反発的固定点であることが分かります。
複素数の定数Cを含んだ複素力学系f(z) = z^2 + Cを考えます。これまでと同じようにある初期値z_0を与えて、くり返しfを作用させて、点の動きを見ていきます。すると、その挙動はz_0とCの値によってさまざまに変わってきます。その中で、ある定数Cに対して点を発散させないような初期値z_0全体の集合を、定数Cに対する充填ジュリア集合(※)と言います。逆に、ある初期値z_0に対して点を発散させないような定数C全体の集合を、初期値z_0に対するマンデルブロ集合と言います。(※単に「ジュリア集合」と言うと、充填ジュリア集合の境界のことを指します。)
z^2 + Cという形以外の定数を含んだ複素関数の場合もしばしば考察されますが、この形が最もよく例に挙げられます。また、マンデルブロ集合は、この関数においてz_0 = 0に対する場合が非常に有名で、単に「マンデルブロ集合」と言うとその場合のことだけを指すこともあります。
定義の中で「発散させない」というのは、収束・振動・カオスのいずれかに至る(=周期が1から∞までのいずれかの周期点に収束する)という意味ですが、最終的に発散するかどうかを判断するのは、実は容易ではありません。というのも、100回目まで計算して発散しないように見えても、200回目まで計算したら発散するかもしれないのです。特にカオス状態は将来の予測がほぼ不可能なため、100回目まで計算した時点では、200回目のことは全く分からないのです。そのため、コンピュータなどで充填ジュリア集合やマンデルブロ集合を求める際は、計算回数の上限をあらかじめ決めておいて、その回数まで計算しても発散しなければ発散しない(すなわち集合に属する)と結論付けます。当然、この場合の計算結果は近似的なものになりますが、実用上はおおむねこれで十分です。
複素力学系f(z) = z^2 + Cにおける、C = 0に対する充填ジュリア集合を考えてみます。実はこれは、先ほど図3で示したf(z) = z^2のアトラクタz = 0の引力圏に他なりません(※)。その範囲から初期値z_0を選べば発散しないという領域のことです。(※正確には、z = 0の引力圏は境界を含みませんが、充填ジュリア集合は周期∞までの全ての周期点の引力圏を合わせたものなので、境界を含みます。)
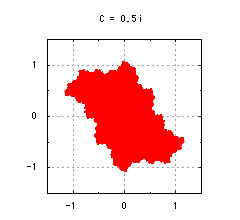
図4-
C = 0.5iの充填ジュリア集合
では、例えばC = 0.5iの場合の充填ジュリア集合はどうなるでしょうか?図4をご覧ください。
ただの円板だったものが、とたんに複雑で奇妙な形になりました。この充填ジュリア集合の境界線はギザギザしていますが、これはどんなに拡大しても平坦になりません。永遠に微細な構造が現れ続けます。さらに特徴的なのは、拡大するごとに、全体の形や他の部分と似たような形が何度も現れます。このように拡大しても複雑さが変わらず、部分と全体が相似な性質を持った図形をフラクタルと呼びます。
このように、単純な式からフラクタル的で非常に複雑な図形が出現するというのが、f(z) = z^2 + Cがしばしば考察の対象に選ばれる理由の一つになっています。これはf(z) = z^2がただの円しか生成しなかったのとは対照的です。
Cを0以外の値に選んだ場合、固定点や周期点の位置も複雑になります。例えば固定点は、z^2 + C = zより、
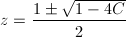 … (式6)
… (式6)
となります。また、2-周期点は、(z^2 + C)^2 + C = zより、
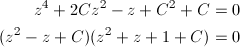 … (式7)
… (式7)
となり、固定点を除外すると、
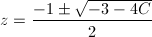 … (式8)
… (式8)
が得られます。
充填ジュリア集合は、周期∞までの周期点のうち、アトラクタとなるものの引力圏(すなわちz_0の範囲)を全て合わせたものです。ちなみに、各周期の周期点がアトラクタとなりうるCの範囲を全て合わせると、次に説明する有名なz_0 = 0に対するマンデルブロ集合となります。ジュリア集合とマンデルブロ集合は定義を混同しやすいので、今z_0とCのどちらを固定して、どちらの範囲を描いているのかを考えるように注意して下さい。(※以降では、充填ジュリア集合を赤色、マンデルブロ集合を青色で描くように統一しています。)
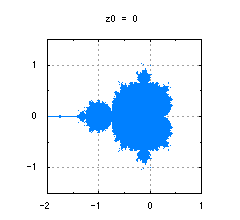
図5-
z_0 = 0のマンデルブロ集合
それでは、お待たせしました。最も有名な、複素力学系f(z) = z^2 + Cのz_0 = 0に対するマンデルブロ集合を描いたものが、図5です。
マンデルブロ集合は、点を発散させない定数Cの範囲を描いたものでした。つまり、z_0 = 0から始める場合に、Cをこの範囲から選べば発散しない(=周期が1から∞のいずれかの周期点に収束する)ということです。よく見かけるマンデルブロ集合のグラフィックには、集合の外側の領域(つまり点を発散させるCの範囲)にカラフルな色がつけられていることが多いですが、これはそのCを選んだ場合に点が発散していく速度によって色分けをしている場合が多いです。他にもいろいろなパラメータによって集合の内外の色付けが可能で、CGアートの一種としても認められています。
このマンデルブロ集合もフラクタル図形です。フラクタル図形の代名詞といっても過言ではないでしょう。その境界線は、どんなに拡大しても決して平坦にならず、この特徴的な形と同じ形がフラクタルな境界線の微細な部分のあちこちに無限に散りばめられています。
同一の複素力学系のマンデルブロ集合とジュリア集合の間には密接な関係があります。これまで見てきた複素力学系f(z) = z^2 + Cでは、初めにマンデルブロ集合を描いた後、その各点におけるCの値とって充填ジュリア集合を描いていくと、さまざまな充填ジュリア集合に出会うことができます。
図6には、マンデルブロ集合の特徴的な部分のCに対する充填ジュリア集合を描いてみました。このように、充填ジュリア集合の形は、Cによって、さまざまに変化します。実軸上の充填ジュリア集合は上下対称になっており、また、Cの虚部の正負が反転するとジュリア集合も上下反転しています。さらに、マンデルブロ集合の境界に近い点ほど、微細でカオス的な構造が出現します。
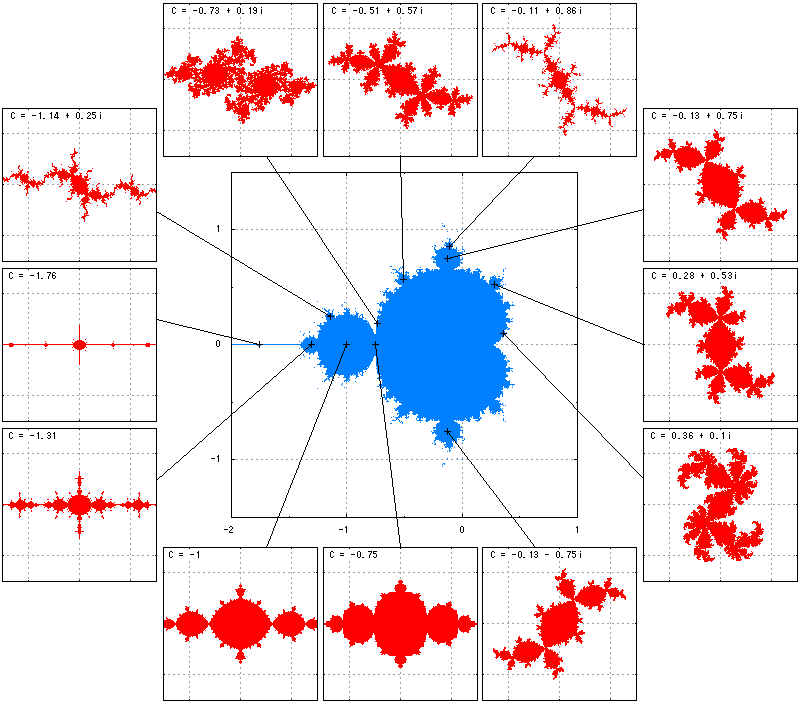
図6-複素力学系f(z) = z^2 + Cでのマンデルブロ集合と充填ジュリア集合の相関
他の複素力学系のマンデルブロ集合にはどのようなものがあるでしょうか。f(z) = z^2 + Cの指数部分を2以上の整数kに一般化したf(z) = z^k + Cを考えてみましょう。z_0はいずれも0がよく選ばれます。実際に描いてみると、指数を増やしていくごとにこぶの数が増えていきます。図7には、kを2から8まで変化させた場合のマンデルブロ集合と、+印の点における充填ジュリア集合を描きました。ちなみに、非整数のkを選ぶことも数式上は可能ですが、その場合はなんとも言えない中途半端な形が現れます。また、k = 1の場合は、マンデルブロ集合はC = 0の一点につぶれてしまいます。
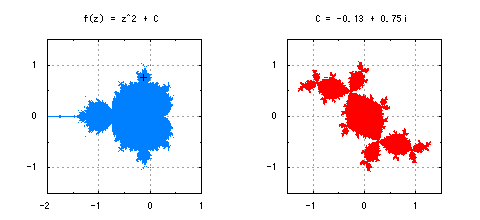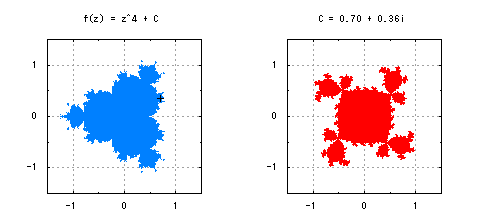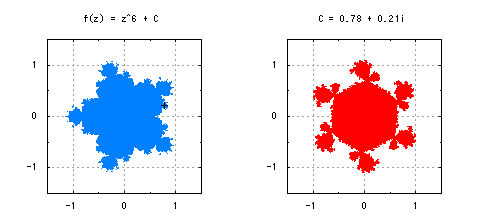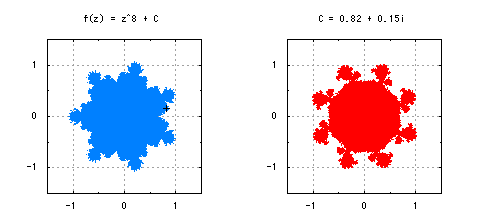
図7-複素力学系f(z) = z^k + Cにおけるマンデルブロ集合と充填ジュリア集合
最後に、もう一つ別の複素関数を紹介しておきます。f(z) = Cz(1 - z^k)もまたしばしば考察される複素関数の一つです。この場合、z_0を(k + 1)^{-1/k}と選ぶと、図8のような少しこれまでと違った形のマンデルブロ集合が描かれます。こちらもフラクタル図形です。
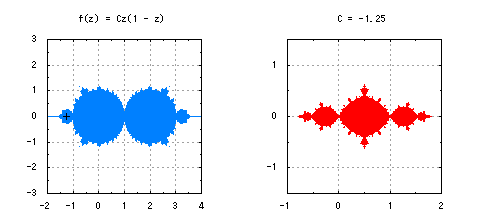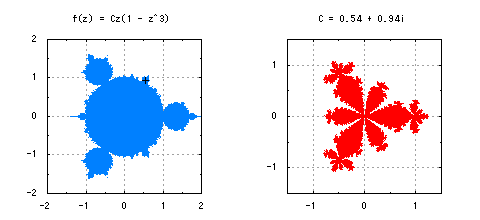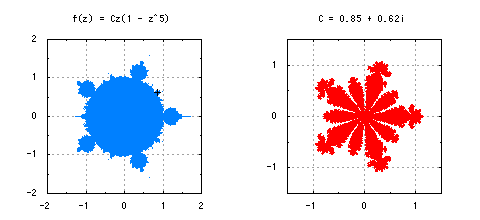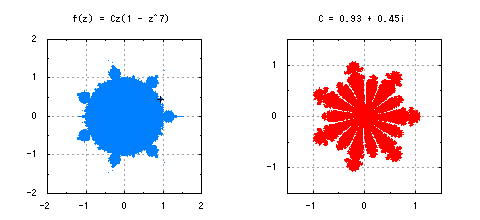
図8-複素力学系f(z) = Cz(1 - z^k)におけるマンデルブロ集合と充填ジュリア集合
主な参考文献
- 芹沢 浩「複素数とフラクタル」、東京図書、1995年(ISBN 9784489004667)
更新履歴
- 2012/09/23 - 初版完成。
- 2012/10/08 - 参考文献を加筆。