概要
根号(√記号)は、本来正の実数に対する演算子で、その2つの平方根のうち正の方を表すものでした。これが、負の実数に拡張され、-1の平方根うちの片方を虚数単位iとおくことによって、x < 0の場合は、
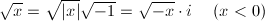 … (式1)
… (式1)
と定義されました。
それでは、一般の複素数に対する根号はどのように定義されているのか確認してみましょう。
数学自由研究 > 複素数に対する根号
根号(√記号)は、本来正の実数に対する演算子で、その2つの平方根のうち正の方を表すものでした。これが、負の実数に拡張され、-1の平方根うちの片方を虚数単位iとおくことによって、x < 0の場合は、
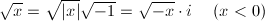 … (式1)
… (式1)
と定義されました。
それでは、一般の複素数に対する根号はどのように定義されているのか確認してみましょう。
複素数zに対して、その偏角をθ、絶対値をrとします。偏角は-π < θ ≤ πとします。
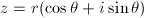 … (式2)
… (式2)
いわゆる複素数の極形式です。ここで、√{z}とは、一般に次のように定義されています。
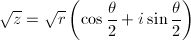 … (式3)
… (式3)
-π/2 < θ/2 ≤ π/2ですから、√{z}の実部は必ず0か正であることが分かります。また、-π < θ < πではθとsinθの符号が一致するため、zと√{z}の虚部は符号が等しいことも分かります。θ = π、すなわちzが負の実数の場合は、θ/2 = π/2なので、虚部は正となります。まとめると、表1の通りとなります。
| zの実部 | zの虚部 | zの偏角 | √{z}の実部 | √{z}の虚部 | √{z}の偏角 |
|---|---|---|---|---|---|
| + | + | (0, π/2) | + | + | (0, π/4) |
| - | + | (π/2, π) | + | + | (π/4, π/2) |
| 0 | + | π/2 | + | + | π/4 |
| + | - | (-π/2, 0) | + ※ | - ※ | (-π/4, 0) |
| - | - | (-π, -π/2) | + ※ | - ※ | (-π/2, -π/4) |
| 0 | - | -π/2 | + ※ | - ※ | -π/4 |
| + | 0 | 0 | + | 0 | 0 |
| - | 0 | π | 0 | + | π/2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
ちなみに、もし偏角を0 ≤ θ < 2πで定義した場合は、0 ≤ θ/2 < πより、√{z}の虚部が必ず0か正となります。一方、√{z}の実部は、zの虚部と符号が一致することになります。これらは、表1の※の部分の正負が逆転することになります。
以降は紛らわしいので、-π < θ ≤ πの場合で考えるものとします。
極形式での定義は分かりやすく簡単なものでしたが、通常の直交形式ではどうなるでしょうか。
今a、b、c、dを実数として、
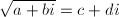 … (式4)
… (式4)
としたとき、cとdをaとbおよび正の実数に対する根号の定義だけで表してみます。表1より、c ≥ 0であり、またb ≠ 0の場合は、bとdの符号が等しいはずです。
まず、両辺を2乗して実部と虚部をそれぞれ比較すると、
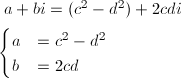 … (式5)
… (式5)
を得ます。ここで、bの正負によって場合分けをします。
b = 0の場合、b = 2cdより、cとdのいずれかまたは両方が0のはずです。これは通常の実数に対する根号の定義です。 cとdは定義よりいずれも実数なので、c^2、d^2ともに0以上ですから、aの正負によって次のようになります。a < 0のとき、-aは正の実数となることに注意して下さい。
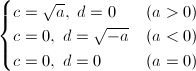 … (式6)
… (式6)
b > 0の場合、b = 2cdより、cとdはいずれも0ではなく、かつ符号が等しいはずです。d = b / 2cより、
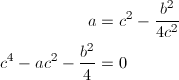 … (式7)
… (式7)
となるので、c^2に関する二次方程式として解くと、
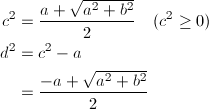 … (式8)
… (式8)
を得ます。表1より、c、dともに正ですので、結局、
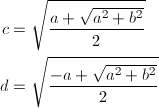 … (式9)
… (式9)
となります。この定義は、a < 0のとき√{a^2} = -aとなることなどに注意すれば、先のb = 0の場合の結果にも当てはめることができます。
b = 2cdより、cとdはいずれも0ではなく、かつ符号が異なるはずです。
b > 0の場合と同様にして、
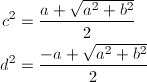 … (式10)
… (式10)
を得ますが、表1より、cは正、dは負となるので、
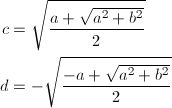 … (式11)
… (式11)
となります。
以上を全てまとめると、以下のようになります。
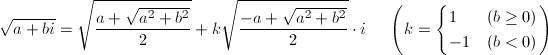 … (式12)
… (式12)
上式右辺の根号の中身は、全て0か正の実数になります。特にb = 0の場合は、一般の実数に対する根号の定義として、
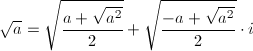 … (式13)
… (式13)
を得ます。