テンパズルの解の探索
4つの1桁の自然数と四則演算のみを使って数を作るというパズルがあります。作る数はしばしば10とされることから、Wikipediaによると「テンパズル(10 puzzle)」や「メイクテン(make 10)」などと呼ばれているそうです。
細かいルールの違いがいろいろあるようですが、今回は以下のルールのテンパズルを取り扱いと思います。
・相異なる4つの1桁の数を使う。0は使わない。
・4つの数を使う順序は問わない。
・複数の数をつなげて2桁以上の数として使うことはできない。
・使える演算子は、+、-、×、÷のみとする。()は必要に応じて何回でも使用可能。
例えば、{2,3,4,5}という4つの数が与えられたときは、10 = 2×(4-3)×5が答え(の一つ)となります。
順序を問わない相異なる4つの1桁の自然数の組み合わせというのは、9C4 = 9×8×7×6/4! = 126通りあります。解は複数あることもあれば、存在しない場合もあります。10を作る場合は、上記のルールに従う限り、126通り全てに解が存在することが知られています。
さて、126通りの数の組合せ全てに対してパズル感覚で挑戦していくのは、相当な頭の体操になって暇つぶしには最適でしょうが、通常は気が遠くなってしまいます。そこで、ここはコンピュータを使って総当たり的に解を探していきます。
2つの数XとYに四則演算を作用させる場合、次の6通りの結果が考えられます。
X+Y X-Y Y-X X×Y X÷Y Y÷X
引き算と割り算は可換ではないので、逆にした場合も考えています。
テンパズルでは、4つの数を使うので、二項演算である四則演算は必ず3回使われます。先の6種類の演算のいずれかを◇で表すと、3回の使われ方は、次の2通りです。
(A◇B)◇C)◇D
(A◇B)◇(C◇D)
後置記法(逆ポーランド記法)で書くと、
D C B A ◇ ◇ ◇
D C ◇ B A ◇ ◇
の2通りとなります。
この中のA、B、C、Dの4ヶ所への数の当てはめ方は、4! = 24通りありますが、上の場合、AとBを逆にしたものは考える必要がないため、24/2 = 12通りで十分です。下の場合は、AとBを逆にしたもの、CとDを逆にしたもの、さらに(A◇B)と(C◇D)を丸ごと逆にしたものも考える必要がないため、24/2/2/2 = 3通りで十分です。したがって、演算子と数の順序は合計15通りを考えます。
以上より、15通りの計算順序に対し、3ヶ所の演算に6^3 = 216通り、4つの数字の組合せとして126通りなので、15×216×126 = 408240通りを計算すれば、総当たりの探索ができると考えられます。それでもなお解が見つからなければ、その組合せでは作れないと結論付けることができると思います。ちなみに、現代のパソコンでは、この程度の量の計算は一瞬でできます。
なお、この方法では、結果として足し算の順序が違うだけのものなど、重複と考えられる解を多く含む可能性がありますが、今回はそれらを排除するところまではやりません。
作る数をNとした場合、横軸にNを、縦軸にNを作れない(解が存在しない)4つの数字の組合せの個数m (0 ≤ m ≤ 126)をとったグラフが図1、mの小さいNをまとめたものが表1です。N = 10のときm = 0であることは、すでに説明した通りです。
表1-解のない組合せの個数が少ないN
| 作る数N |
解のない組合せの個数m |
| 2, 3, 4, 10 | 0 |
| 6, 12 | 1 |
| 24 | 2 |
| 5 | 3 |
| 7, 16 | 4 |
| 1 | 5 |
| 8, 9, 11, 15, 18, 20 | 6 |
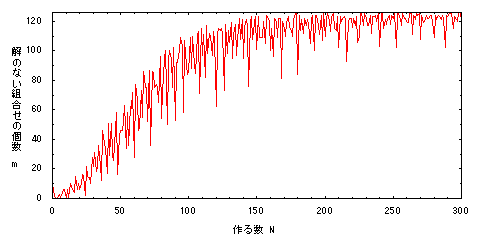
図1-作る数と解の存在しない組合せの個数
N = 10の他にm = 0となる(全ての組合せで解が存在する)ようなNは、他に2、3、4があり、10と合わせて4つで全てのようです。mが0ではないが5以下であるようなNとしては、1、5、6、7、12、16、24があります。24より大きい数で、mが小さい(解の存在しない組合せが少ない)Nは見つかりません。解が全く存在しない(m = 126となる)最も小さいNは、298のようです。
N = 10は必ず解が存在するという点で、パズルとして適した数字と考えられます。解を持つ組合せが少ない(mが大きい)Nを作ろうとすると、その組合せで解を見つけられないだけなのか、解が本当に存在しないのか分からず、パズルとしては楽しめなくなってしまいます。
実際に適当に相異なる4つの数を選んで10作りに挑戦すると、たいていは誰でも数分もかからずに解を見つけられます。しかし、中には紙やペンを使って何時間考えてもなかなか見つからない超難問も存在するのです。最も難しいと考えられるのが、{3,4,7,8}の組合せです。この4つの数字と四則演算から10を作る式を見つけるのは、なかなか大変です。しかも答えはただ1通りしかありません。
他にも、総当たり探索を行うと、人間には到底思いつかない式が見つかったりします。
表2-思いもよらぬ解が存在する組合せ
| 組合せ | 一般の人が比較的簡単に見つけられるであろう解 | 思いもよらぬ解 |
|---|
| {1, 4, 6, 9} |
6+9-1-4 |
4×(9÷6+1) |
| {1, 5, 8, 9} |
5×(1+9-8), (1+9)÷5+8 |
8÷(9÷5-1) |
| {2, 4, 5, 9} |
2+4+9-5 |
5÷(9÷2-4) |
| {2, 5, 6, 9} |
2+5+9-6, (5+6+9)÷2 |
5÷(2-9÷6) |
| {3, 4, 6, 7} |
4×(7-3)-6, 4×7-3×6, 6×7÷3-4 |
6×(4-7÷3) |
| {3, 4, 6, 9} |
3+4+9-6, 6×(9-4)÷3, (4×9-6)÷3 |
3×(4-6÷9) |
| {3, 4, 7, 8} |
なし |
8×(3-7÷4) |
しかし、実は何をもって難問とするかは、難しい問題です。単純に解の種類の個数等では難易度を定量化することはできません。例えば、表2で示したように、途中で非整数を経由しなければならない式は、なかなか思いつかないのではないでしょうか。さらに、解がそのような式しかない場合は、難易度が高いと言えると思います。
作る数を10以外に変えても、表1で示したような、ほとんどの組合せで解が存在する数であれば、難易度が大きく変わることはありません。10作りに飽きたら他の数を作ることで、パズルを楽しみ続けることができます。
一方で、やはり難問も存在します。表3には、10以外の数を作る場合に、非常に主観的ではありますが難しいと思われる問題をまとめてみました。逆に、ここに挙げていないものは、すぐに答えが見つかるはずです。6や12を作る場合は、それぞれ解のない1つを除いては、特に難しいと思われる問題は見つかりませんでした。
表3-10以外の数での難問と解なしの組合せ
| 作る数N | 問題 | 答え |
|---|
| 2 |
{2, 5, 7, 9} |
5÷(7-9÷2), 9÷(7-5÷2) |
| 3 |
{1, 3, 4, 7} |
7÷(4÷3+1), 4÷(7÷3-1) |
| {1, 4, 5, 9} |
5-(9-1)÷4 |
| {1, 7, 8, 9} |
(7+9)÷8+1, 8÷(9-7)-1 |
| 4 |
{1, 4, 5, 9} |
9÷(5÷4+1), 5÷(9÷4-1) |
| {3, 4, 7, 8} |
(3×8+4)÷7, 4×7-3×8 |
| {4, 5, 8, 9} |
(5×8-4)÷9, 5×8-4×9 |
| 5 |
{1, 4, 5, 9} |
9÷(4÷5+1), 4÷(9÷5-1) |
| {1, 5, 6, 9} | 解なし |
| {3, 5, 7, 8} |
8÷(3-7÷5), 7÷(3-8÷5) |
| {4, 5, 7, 9} | 解なし |
| {4, 5, 8, 9} | 解なし |
| 6 |
{6, 7, 8, 9} | 解なし |
| 難問は特になし |
| 12 |
{1, 5, 7, 8} | 解なし |
| 難問は特になし |
| 16 |
{1, 3, 7, 9} | 解なし |
| {1, 4, 7, 9} |
(7×9+1)÷4 |
| {1, 5, 6, 7} | 解なし |
| {1, 6, 7, 9} | 解なし |
| {2, 3, 5, 8} |
8÷(3-5÷2) |
| {3, 7, 8, 9} | 解なし |
| 24 |
{1, 3, 4, 6} |
6÷(1-3÷4) |
| {1, 4, 5, 6} |
4÷(1-5÷6), 6÷(5÷4-1) |
| {1, 6, 7, 8} | 解なし |
| {3, 4, 6, 7} | 解なし |
更新履歴
- 2012/09/15 - 初版完成。
- 2012/10/08 - 参考文献を加筆。
