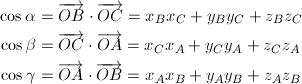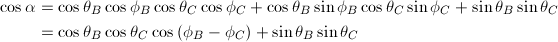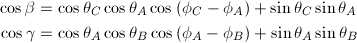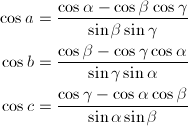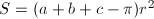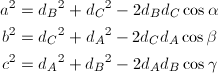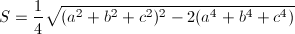冬の夜空に明るく輝く冬の大三角形。何光年も離れた星を結んでできた宇宙空間に浮かぶ超巨大な三角形…いったい面積はいくらだろう?そんな疑問からこの考察は始まりました。冬の大三角と夏の大三角の“面積”を求めてみます。
まず、それぞれの三角形を構成する星々の緒元ですが、今回は表1の値を使います。
表1-夏の大三角と冬の大三角を構成する星の緒元
| |
星の名前 |
赤経φ |
赤緯θ |
赤経φ[rad] |
赤緯θ[rad] |
距離[光年] |
| 夏の大三角 |
A: | アルタイル |
19h 50m 47.0s | +08゚ 52' 06" |
n/a | n/a |
16.77 |
| B: | ベガ |
18h 36m 56.3s | +38゚ 47' 01" |
n/a | n/a |
25.27 |
| C: | デネブ |
20h 41m 25.9s | +45゚ 16' 49" |
n/a | n/a |
1600 |
| 冬の大三角 |
A: | シリウス |
06h 45m 08.9s | -16゚ 42' 58" |
n/a | n/a |
8.6 |
| B: | プロキオン |
07h 39m 18.1s | +05゚ 13' 29" |
n/a | n/a |
11.4 |
| C: | ベテルギウス |
05h 55m 10.3s | +07゚ 24' 25" |
n/a | n/a |
640 |
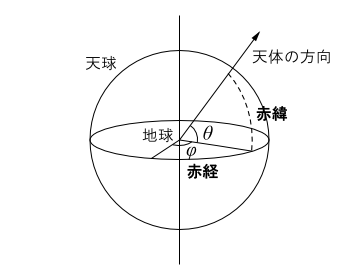
図1-赤経と赤緯
赤経と赤緯は角度(方角)を表すものですが、そのままでは扱いにくいので、ラジアン(rad)に変換しています。赤経は時(h)に換算してからπ/12を、赤緯は度(゚)に換算してからπ/180をかければラジアンになります。
赤経と赤緯は、球座標の一種です(図1)。赤経は通常の球座標の方位角に相当するものですが、赤緯は(90゚ - 天頂角)に相当するものです。したがって、直交座標(x,y,z)との関係は、原点からの距離をrとすると、
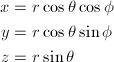 … (式1)
… (式1)
となります。
星までの距離は、赤経や赤緯と比べて正確な値が得られてない場合があります。例えば、デネブやベテルギウスは、地球からの距離が遠いため、年周視差が小さく、大まかな距離しか得られていません。文献によっても値に差があるため、今回は、デネブは1600光年、ベテルギウスは640光年としました。
天球上での面積を求める際は、距離は必要ありません。宇宙空間での面積を求める際に使います。
まずは天球上での面積です。一般に星座の面積といった場合、こちらを指すと思います。地球からその星座を見張る立体角の大きさをその星座の面積とします。立体角とは、「立体的に見張る角度」のことですが、天球上からその星座が切り取る表面積とも言えます。プラネタリウムで球状のスクリーンにその星座を投影したときの大きさと考えれば分かりやすいでしょう。
この場合の“面積”として求められた値は、「全天に対していくらか」という相対的な量になります。
球面上の三角形の面積は、3つの内角の大きさが分かれば、簡単な公式から求めることができます。平面上の三角形と異なり、内角の和は常に180度よりも大きく一定ではないので、3つの内角全てを知る必要があります。
内角の大きさは、球面三角法により、3つの辺の長さから求めることができます。球面上では、辺は球の大円の弧になりますから、辺の長さは弧の中心角で表されます。弧の中心角は、辺の両端の点を表す位置ベクトルの内積を取ることで得られます。
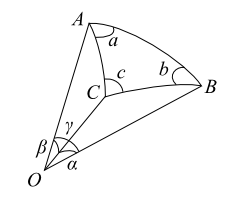
図2-球面上の三角形
今、図2のように、原点をO、単位球面上の3つの点をA、B、C、それぞれの角の大きさをa、b、cとします。また、弧BCの中心角をα、弧CAの中心角をβ、弧ABの中心角をγとします。
弧の中心角の大きさは、両端の点を表す位置ベクトルの内積によって得られます。
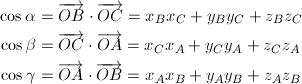 … (式2)
… (式2)
球座標と直交座標の関係(式1)から、
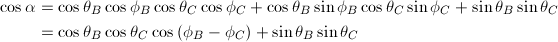 … (式3)
… (式3)
同様に、
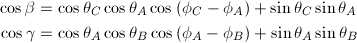 … (式4)
… (式4)
なお、3つの点は全て単位球面上にあると仮定しているので、中心からの距離rはいずれも1として消去しています。
これで、3つの辺の中心角の余弦が求められます。同時に正弦も求めておきます。
表2-天球上での各三角形の辺の中心角
| |
辺 | 中心角 | cos | sin |
| 夏の大三角 |
BC | α |
n/a | n/a |
| CA | β |
n/a | n/a |
| AB | γ |
n/a | n/a |
| 冬の大三角 |
BC | α |
n/a | n/a |
| CA | β |
n/a | n/a |
| AB | γ |
n/a | n/a |
3つの辺の中心角が分かると、球面三角法により、球面の三角形の角の大きさが分かります。球面余弦定理により、以下が成り立ちます。これで得られる値の逆余弦を取れば、それぞれの角の大きさを求められます。
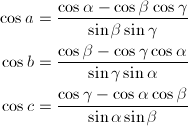 … (式5)
… (式5)
表3-天球上での各三角形の角の大きさ
| |
角 | cos | rad | 度(参考) |
| 夏の大三角 |
a | n/a |
n/a | n/a |
| b | n/a |
n/a | n/a |
| c | n/a |
n/a | n/a |
| 冬の大三角 |
a | n/a |
n/a | n/a |
| b | n/a |
n/a | n/a |
| c | n/a |
n/a | n/a |
以上でめでたく3つの角の大きさa、b、cが求まりました。冬の大三角は、3つの角の大きさがほとんど同じで、正三角形に近いことが分かりますね。
最後に、球面上での三角形の面積Sは、以下のようにして求められます。
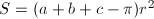 … (式6)
… (式6)
この公式の導出は割愛しますが、次のように考えると簡単に導くことができます。三角形の一つの点を軸として、辺に沿ってその球をスイカのように切り分けることを想像して下さい。その切り分けたスイカの皮の面積は、球全体の表面積と三角形の角度から簡単に求められますが、これを3つの点について全て足すと、球全体の表面積と求める三角形の面積を複数回足し合わせたものと等しくなります。ここから式を立てて整理すると、この公式が得られます。
ここで、r = 1(単位球)とした場合がステラジアン(str)、r = 180 / πとした場合が平方度での値になります。ステラジアンも平方度も立体角の単位ですが、星座の大きさを表すときは一般に平方度がよく使われるようです。また、rに関係なく、Sを4πr^2(全天の面積)で割れば、全天に占める割合となります。
表4-天球上での各三角形の面積
| |
面積[str] | 面積[平方度] | 全天に対する% |
| 夏の大三角 |
n/a |
n/a |
n/a |
| 冬の大三角 |
n/a |
n/a |
n/a |
以上により、夏の大三角は約418.1平方度で全天の約1.01%を、冬の大三角は夏の大三角より少し小さい約286.7平方度で全天の約0.695%を、それぞれ占める三角形であるということが分かりました。
ちなみに、現在最も大きな星座と言われるうみへび座は、約1303平方度だそうです。
次は、宇宙空間での面積です。3つの星の天球上での位置ではなく、宇宙空間での実際の位置を結んでできる三角形の面積を考えます。この値自体はあまり実用的な意味を持たないと思いますが、宇宙の広大さを実感できるので私は気に入っています。なお、面積の計算の際に、宇宙空間の歪みや星自身の大きさなどは考えないことにします。
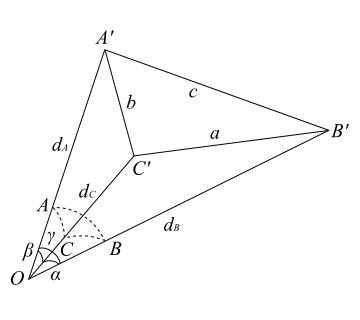
図3-宇宙空間の三角形
今、図3のように、先ほど単位球面上で考えた三角形の3点を、実際の距離まで延長し、それぞれA'、B'、C'とします。また、辺B'C'の長さをa、C'A'をb、A'B'をcとし、原点からA'、B'、C'までの距離をそれぞれd_A、d_B、d_Cとします。
三角形の面積は、3辺の長さを求めてヘロンの公式で算出することにします。辺の長さは、両端の星と地球を結ぶ三角形を考えると、2つの星までの距離と、そのなす角度から、通常の余弦定理で求めることができます。
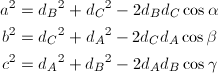 … (式7)
… (式7)
星までの距離は最初に示した表の通りですし、角度(の余弦)は、先ほど天球上での面積を求める際にすでに求めましたので、3辺の長さは、次のように求められます。
表5-各三角形の実際の辺の長さ
| |
辺 | 長さ[光年] |
| 夏の大三角 |
a |
n/a |
| b |
n/a |
| c |
n/a |
| 冬の大三角 |
a |
n/a |
| b |
n/a |
| c |
n/a |
天球上での場合と異なり、実際はものすごい細長い形の三角形であることが分かります。
三角形の3辺の長さが求められたので、ヘロンの公式を用いて面積Sを求めます。
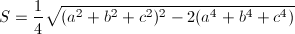 … (式8)
… (式8)
表6-各三角形の実際の面積 (1)
| |
面積[平方光年] |
| 夏の大三角 |
n/a |
| 冬の大三角 |
n/a |
1平方光年は、1光年×1光年の正方形の面積です。実感がわかないので、他の単位にも換算してみましょう。1光年はそれぞれ、約63241.0771AU(天文単位)、9460730472580.8(=9.4607×1012=9兆4607億)kmと等しいので、1平方光年は、約3999433831平方AU、89505421074818927300612528.64(=8.95054×1025=89秭5054垓)km2と同じ面積です。また、地球の公転軌道円(地球が太陽の周りを一周して描く円=π平方AU)の約1273059328倍です。
表7-各三角形の実際の面積 (2)
| |
面積[平方光年] |
面積[平方AU] |
面積[km2] |
地球公転軌道円の何倍か |
| 夏の大三角 |
n/a |
n/a |
n/a |
n/a |
| 冬の大三角 |
n/a |
n/a |
n/a |
n/a |
とてつもない大きさですね。例えば、km2に換算した冬の大三角の面積は、日本語で読むと「12穣3883秭」、英語で読むと「123 octillion and 883 septillion」となります。穣は1兆の1兆倍の1万倍です。地球の公転軌道円の大きさと比べても、冬の大三角は約1兆8000億倍、夏の大三角は約11兆倍もの広さを持つ、超広大な三角形であることが分かりました。
夏の大三角、冬の大三角以外にも、任意の星から成る三角形について、面積を自動で計算するフォームを作りました。以下のフォームに、3つの星の赤経、赤緯、距離を入力すると、天球上での角度と面積、宇宙空間での辺の長さと面積を自動的に算出します。
JavaScriptで計算していますので、64ビット浮動小数点数で表現できる範囲内において計算が可能ですが、あまりに大きな数値は指数表記になります。また、数値以外の文字や不正な値を入力すると、正しく計算できません。ご自身の責任においてご利用下さい。
大きな数の読み方については、Wikipediaの命数法(日本語)や、Names of large numbers(英語)などをご覧下さい。

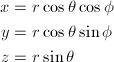 … (式1)
… (式1)