正五角形の辺と対角線の比

導出

正五角形の一辺の長さと対角線の比が黄金比であることは有名ですが、導出の方法を考えてみました。

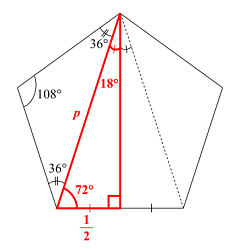
図1-正五角形の辺と対角線で作る三角形

図1のように、正五角形の1つの辺と2つの対角線でできる二等辺三角形と、それを半分にした直角三角形を考えると、対角線の長さと一辺の半分の長さの比は、sin18ﾟに等しいことが分かります。つまり、一辺の長さを1、対角線の長さをpとすると、

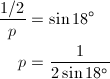$\begin{align*} \frac{1/2}{p}&=\sin{18^\circ} \\ p&=\frac{1}{2\sin{18^\circ}} \end{align*}$ … (式1)

が成り立ちます。そこで、sin18ﾟを求めます。

まず、xとyを以下のようにおきます。

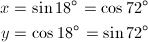$\begin{align*} x&=\sin{18^\circ}=\cos{72^\circ}\\ y&=\cos{18^\circ}=\sin{72^\circ} \end{align*}$ … (式2)

xとyは当然以下の関係式を満たします。

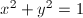x^2+y^2=1 … (式3)

次に、三角関数の二倍角の公式を使ってcos36ﾟとsin36ﾟをxとyで表します。

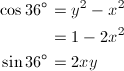$\begin{align*} \cos{36^\circ}&=y^2-x^2 \\ &=1-2x^2 \\ \sin{36^\circ}&=2xy \end{align*}$ … (式4)

さらに、cos72ﾟとsin72ﾟもxとyで表します。

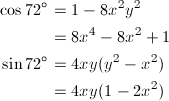$\begin{align*} \cos{72^\circ}&=1-8x^2y^2 \\ &=8x^4-8x^2+1 \\ \sin{72^\circ}&=4xy(y^2-x^2) \\ &=4xy(1-2x^2) \end{align*}$ … (式5)

ここで、cos72ﾟはx、sin72ﾟはyとそれぞれ等しかったわけですから、次の関係式を得ます。

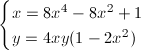$\begin{cases} x=8x^4-8x^2+1 \\ y=4xy(1-2x^2) \end{cases}$ … (式6)

下の式にはyが残っていますが、yは0ではないので、両辺のyは消去できます。整理すると、xに関する次の2つの方程式を得ます。

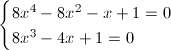$\begin{cases} 8x^4-8x^2-x+1=0 \\ 8x^3-4x+1=0 \end{cases}$ … (式7)

下の式をx倍して、上の式から引くと、

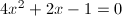4x^2+2x-1=0 … (式8)

となり、高次の項が消えて二次方程式になりました。解の公式およびxは正という条件から、

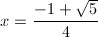$x=\frac{-1+\sqrt{5}}{4}$ … (式9)

がxすなわちsin18ﾟの値として求まります。最初に示した対角線の長さとの関係より、

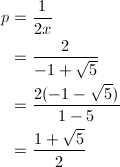$\begin{align*} p&=\frac{1}{2x} \\ &=\frac{2}{-1+\sqrt{5}} \\ &=\frac{2(-1-\sqrt{5})}{1-5} \\ &=\frac{1+\sqrt{5}}{2} \end{align*}$ … (式10)

となって、めでたく黄金比であることが導かれました。