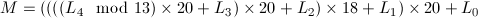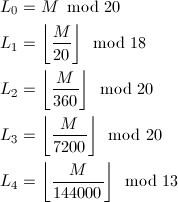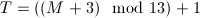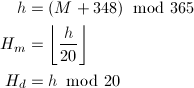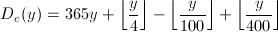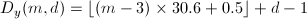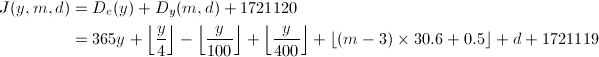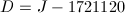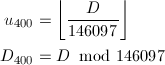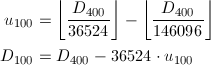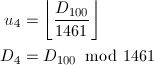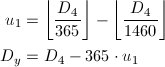マヤ暦のしくみと換算

はじめに

2012年世界終末説で話題となった古代マヤ文明の暦。高度な数学や天文学を持っていたと言われるマヤ文明の暦とはどんなものなのか、興味がわいたので調べてみました。このページでは、マヤの暦の数学的な話と、グレゴリオ暦との変換方法に絞って紹介したいと思います。文化的な側面については、他の文献をご覧下さい。

ページの最後には、マヤの暦とグレゴリオ暦との変換スクリプトを置きました。ぜひご利用下さい。

マヤ日数とユリウス通日

マヤの暦と現在世界中で日常的に使用しているグレゴリオ暦との関係を知るには、まずマヤ日数とユリウス通日という二つの日数が重要になります。

まず、ユリウス通日（Julian day）とは、グレゴリオ暦紀元前4714年11月24日からの日数のことを言います。正確には、真のユリウス通日はその日の正午からの日数ですが、このページでは、これを深夜0時からの日数に修正したもの（CJD: Chronological Julian day）を以降使います。例えば、2000年1月1日のユリウス通日は2451545です。後の節で詳しく述べますが、ユリウス通日とグレゴリオ暦は一対一の関係にあり、グレゴリオ暦からユリウス通日を求めることも、逆にユリウス通日からグレゴリオ暦を求めることも容易にできます。

次に、マヤ日数とは、ユリウス通日から584283を引いたものを言います。この584283という数字は相関定数（correlation）と呼ばれ、グレゴリオ暦とマヤの暦の関係を決める数字で、マヤの長期暦「11.16.0.0.0」がグレゴリオ暦で1539年11月12日にあたるだろうという研究結果から得られたものだそうです。このマヤ日数からマヤの各種の暦が計算されます。

マヤの暦をグレゴリオ暦に換算するには、マヤの暦をマヤ日数に換算し、マヤ日数を相関定数を用いてユリウス通日に換算し、そしてユリウス通日をグレゴリオ暦に換算します。マヤの暦とマヤ日数の換算と、ユリウス通日とグレゴリオ暦の換算は、数学的に矛盾なく行うことができますが、マヤ日数とユリウス通日の換算は、相関定数の選び方によって結果が異なってしまいます。実は、584283という数字も現在のところ最も有力な説であるというだけに過ぎません。それが本当に正しいかはおそらく誰も分からないでしょう。他にも584285とする説など、さまざまな相関定数が考案されていますが、このページでは以降584283を採用したいと思います。2012年世界終末説も、この相関定数によるものです。

マヤの長期暦

それでは、まずは終末説で話題になったマヤの長期暦（Long count calendar）から見ていきます。

長期暦は、Baktun、Katun、Tun、Uinal、Kinという5種類の単位で表した5つの数字を、この順にドットでつないで表します（注：これは現代の表記法です。当時のマヤ文明には、独自の文字による独自の表記法がありました）。それぞれの単位の意味や数字の範囲は次の表1の通りです。※表中の「変数」は、当ページの数式で用いた変数の名前です。

表1-長期暦に使用する5つの単位
単位	読み方	換算	日数	値の範囲	変数※
Baktun	バクトゥン	= 20Katun	144000	0～12（0は13とも書く）	L_4
Katun	カトゥン	= 20Tun	7200	0～19	L_3
Tun	トゥン	= 18Uinal	360	0～19	L_2
Uinal	ウイナル	= 20Kin	20	0～17	L_1
Kin	キン	= 1日	1	0～19	L_0

長期暦は、13.0.0.0.0から始まり、13.0.0.0.1、13.0.0.0.2、と続き、12.19.19.17.19の翌日がまた13.0.0.0.0に戻ります。このしくみは、時計の11時59分の1分後が12時00分に戻るのとよく似ています。この長期暦が一周するのにかかるのは、13 × 144000 = 1872000日、実に約5125年にもおよびます。前回、13.0.0.0.0だった日は、マヤ日数0だった日で、グレゴリオ暦では紀元前3114年8月11日にあたります。この次に13.0.0.0.0となる日が、そうです、マヤ日数1872000のグレゴリオ暦2012年12月21日というわけなのです。

長期暦からマヤ日数Mを求めるのは簡単です。時・分・秒で表された時刻を秒数に換算するのと同じ原理です。以下の式で、modは余り演算です。

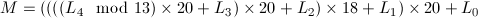
$M=((((L_4\mod 13)\times 20+L_3)\times 20+L_2)\times 18+L_1)\times 20+L_0$

ただし、長期暦は循環するので、どの周期を求めているかに注意しなければなりません。紀元前3114年に始まった周期を計算する場合は、上記の式で問題ありませんが、2012年に始まった次の周期を計算する場合は、上記式の計算結果に1872000を加える必要があります。

逆に、マヤ日数Mから長期暦は、以下のように求められます。modは余り演算、⌊ ⌋は床関数です。

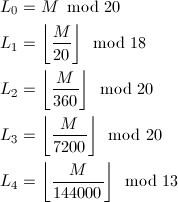
$\begin{align*} L_0&=M\hspace{-2mm}\mod 20\\ L_1&=\left\lfloor\frac{M}{20}\right\rfloor\hspace{-2mm}\mod 18\\ L_2&=\left\lfloor\frac{M}{360}\right\rfloor\hspace{-2mm}\mod 20\\ L_3&=\left\lfloor\frac{M}{7200}\right\rfloor\hspace{-2mm}\mod 20\\ L_4&=\left\lfloor\frac{M}{144000}\right\rfloor\hspace{-2mm}\mod 13 \end{align*}$

マヤの260日暦

長期暦とは別に、もっと短い周期の暦も使用されていました。その一つが260日暦（Tzolkin、ツォルキン）です。

260日暦は、1～13の「係数」と、20種類の「日の名称」の組合せで一つの日を表します。日の名称は、長期暦のKinと対応しており、表2のようになっています。

表2-260日暦の日の名称
Kin	日の名称	読み方	Kin	日の名称	読み方
1	Imix	イミシュ	11	Chuen	チュエン
2	Ik	イック	12	Eb	エッブ
3	Akbal	アクバル	13	Ben	ベン
4	Kan	カン	14	Ix	イシュ
5	Chicchan	チクチャン	15	Men	メン
6	Cimi	キミ	16	Cib	キッブ
7	Manik	マニック	17	Caban	カーバン
8	Lamat	ラマット	18	Etzunab	エツナッブ
9	Muluc	ムルック	19	Cauac	カワック
10	Oc	オック	0	Ahau	アハウ

係数も日もどちらも毎日1ずつ進んでいきます。つまり、1Imixの翌日は、2Ikとなります。係数は13で一周し、日は20で一周するため、13と20の最小公倍数である260日で両者の組合せが最初と同じに戻ります。これが260日暦と呼ばれる所以です。これは、例えるなら、干支（十干と十二支の組合せ）が10と12の最小公倍数である60年で一周する（還暦）のとよく似ています。

マヤ日数0の日の260日暦は、4Ahauでした。したがって、係数Tはマヤ日数Mを用いて次のように求められます。

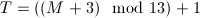
$T=((M+3)\mod 13)+1$

マヤの365日暦

短い周期の暦はもう一つあります。それが365日暦（Haab、ハアブ）です。

365日暦は、0～19の「日」と、19種類の「月の名称」の組合せで一つの日を表します。月の名称は、表3のようになっています。

表3-365日暦の月の名称
月	月の名称	読み方	月	月の名称	読み方
0	Pop	ポプ	10	Zac	サック
1	Uo	ウォ	11	Ceh	ケフ
2	Zip	シップ	12	Mac	マック
3	Zotz	ソッツ	13	Kankin	カンキン
4	Tzec	セック	14	Muan	ムアン
5	Xul	シュル	15	Pax	パシュ
6	Yaxkin	ヤシュキン	16	Kayab	カヤッブ
7	Mol	モル	17	Cumku	クムク
8	Ch'en	チェン	18	Uayeb	ワイエブ
9	Yax	ヤシュ

日は毎日1ずつ進み、19日までいくと0日に戻ります。それと同時に月が1つ進みます。つまり、0Popの翌日が、1Pop、2Pop、3Pop、…と続き、19Popの翌日が0Uoとなります。ただし、最後の月であるUayebは、0～4の5日間しかありません。つまり4Uayebの翌日は0Popです。これにより、20 × 18 + 5 = 365日で一周して同じ日に戻ります。これが365日暦と呼ばれる所以です。365日暦は、我々が普段使う通常の月と日のしくみに似ています。ただし、365日暦には、グレゴリオ暦の閏年などのしくみはありません。

マヤ日数0の日の365日暦は、8Cumkuでした。したがって、365日暦の月H_mと日H_dは、マヤ日数Mを用いて次のように求められます。

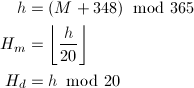
$\begin{align*} h&=(M+348)\hspace{-2mm}\mod 365\\ H_m&=\left\lfloor\frac{h}{20}\right\rfloor\\ H_d&=h\hspace{-2mm}\mod 20 \end{align*}$

マヤの暦は、ここまでに説明した長期暦、260日暦、365日暦の3つを並べて、「13.0.0.0.0 4Ahau 8Cumku」のように表記します。

グレゴリオ暦からユリウス通日への換算

さて、これでマヤの各種の暦は計算できますが、現在我々が使うグレゴリオ暦と換算するには、最初の節で述べた通り、マヤ日数およびユリウス通日を経由しなくてはなりません。そこで、グレゴリオ暦からユリウス通日（CJD）への換算の仕方を紹介します。

まず、計算のための準備です。これ以降、1月と2月は、前年の13月と14月として計算していきます。例えば、2000年1月1日を計算したい場合は、1999年13月1日と読み替えます。こうすることで、グレゴリオ暦の閏日（2月29日）が1年の最後に来るので、数式が簡単になります。また、紀元前y年は、-(y - 1)年と読み替えます（Astronomical year numbering）。例えば、紀元前100年は-99年、紀元前1年は0年です。数字が1ずれている点に注意です。

グレゴリオ暦の閏年配置のルールより、0年3月1日からy年3月1日までの日数D_eは、

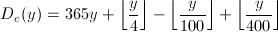
$D_e(y)=365y+\left\lfloor\frac{y}{4}\right\rfloor-\left\lfloor\frac{y}{100}\right\rfloor+\left\lfloor\frac{y}{400}\right\rfloor$

で求められます。一方、同じ年の3月1日からm月d日までの日数D_yは、

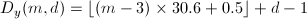
$D_y(m,d)=\left\lfloor(m-3)\times 30.6+0.5\right\rfloor +d-1$

で求められます。ただし、先に述べた通り、「同じ年」とは3月1日から翌年の2月末日までとしているため、mに代入する数字は3～14であることに注意して下さい。

ここで、これらの式を用いて、ユリウス通日0であるグレゴリオ暦紀元前4714年（-4713年）11月24日を計算すると、-1721120を得ます。よって、0年3月1日のユリウス通日は1721120と分かります。

以上より、グレゴリオ暦y年m月d日のユリウス通日Jは、

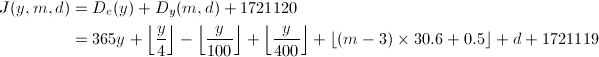
$\begin{align*} J(y,m,d)&=D_e(y)+D_y(m,d)+1721120\\ &=365y+\left\lfloor\frac{y}{4}\right\rfloor-\left\lfloor\frac{y}{100}\right\rfloor+\left\lfloor\frac{y}{400}\right\rfloor+\left\lfloor(m-3)\times 30.6+0.5\right\rfloor +d+1721119 \end{align*}$

となります。

ユリウス通日からグレゴリオ暦への換算

今度は、逆にユリウス通日（CJD）をグレゴリオ暦に換算する方法です。こちらでも先ほどと同じく、1月と2月は前年の13月と14月とし、紀元前の年は負の数で表記していきます。

まず、ユリウス通日Jを、0年3月1日からの日数Dに換算します。

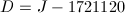
D=J-1721120

Dから400年単位u_{400}と、400年に満たない日数D_{400} (0 ≤ D_{400} < 146097 = 365 × 400 + 97)を求めます。

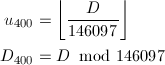
$\begin{align*} u_{400}&=\left\lfloor\frac{D}{146097}\right\rfloor\\ D_{400}&=D\hspace{-2mm}\mod 146097 \end{align*}$

D_{400}から100年単位u_{100} (0 ≤ u_{100} < 4)と、100年に満たない日数D_{100}を求めます。400年に一度の閏年があるため、式がやや変則的になっています。u_{100} = 3の場合は、0 ≤ D_{100} < 36525 = 365 × 100 + 25となり、それ以外では、0 ≤ D_{100} < 36524 = 365 × 100 + 24となります。

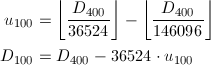
$\begin{align*} u_{100}&=\left\lfloor\frac{D_{400}}{36524}\right\rfloor-\left\lfloor\frac{D_{400}}{146096}\right\rfloor\\ D_{100}&=D_{400}-36524\cdot u_{100}\end{align*}$

D_{100}から4年単位u_4 (0 ≤ u_4 < 25)と、4年に満たない日数D_4 (0 ≤ D_4 < 1461 = 365 × 4 + 1)を求めます。

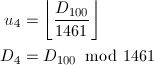
$\begin{align*} u_4&=\left\lfloor\frac{D_{100}}{1461}\right\rfloor\\ D_4&=D_{100}\hspace{-2mm}\mod 1461 \end{align*}$

D_4から1年単位u_1 (0 ≤ u_1 < 4)と、1年に満たない日数D_yを求めます。4年に一度の閏年があるため、式がやや変則的になっています。u_1 = 3の場合は、0 ≤ D_y < 366となり、それ以外では、0 ≤ D_y < 365となります。

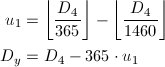
$\begin{align*} u_1&=\left\lfloor\frac{D_4}{365}\right\rfloor-\left\lfloor\frac{D_4}{1460}\right\rfloor\\ D_y&=D_4-365\cdot u_1\end{align*}$

そして、u_{400}、u_{100}、u_4、u_1を用いて、年yを求めます。

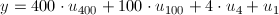
$y=400\cdot u_{400}+100\cdot u_{100}+4\cdot u_4+u_1$

最後に、1年に満たない日数D_yから、月mと日dを求めます。

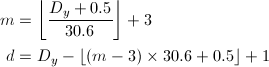
$\begin{align*} m&=\left\lfloor\frac{D_y+0.5}{30.6}\right\rfloor+3\\ d&=D_y-\left\lfloor(m-3)\times 30.6+0.5\right\rfloor+1 \end{align*}$

くり返しになりますが、月は3～14月で計算しています。上式にしたがって計算して、例えば1999年13月1日という結果が出たら、それは2000年1月1日と読み替えます。

各暦の相互変換スクリプト

ここまでに紹介した各暦をJavaScriptで簡単に変換できるようにしました。以下のフォームを編集すると、自動的に他の暦が再計算されます。長期暦から他の暦を計算する際は、長期暦のどの周期を計算しているかに注意して下さい。あまりに遠い過去や未来の日付や、不正な日付、数字以外の文字等を入力すると、正しく計算できません。ご自身の責任においてご利用下さい。

グレゴリオ暦	年月日（？）
ユリウス通日（CJD）
マヤ日数
マヤ暦（長期暦）	. . . .
マヤ暦（260日暦、365日暦）	n/a n/a
長期暦の周期