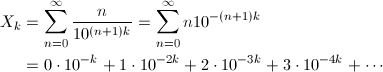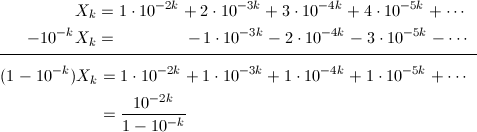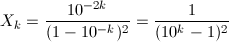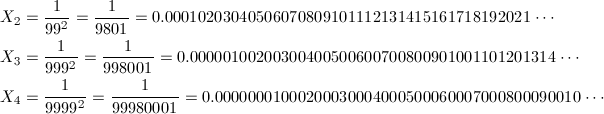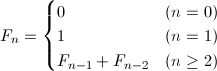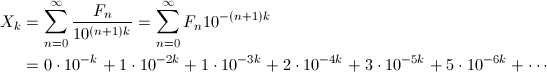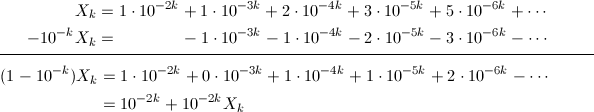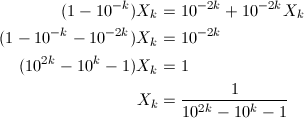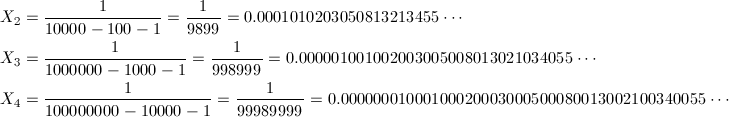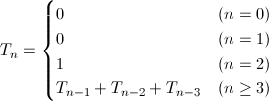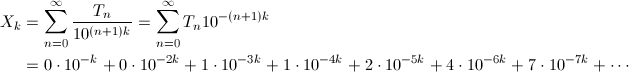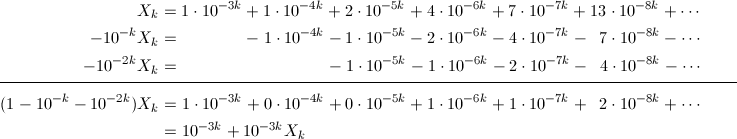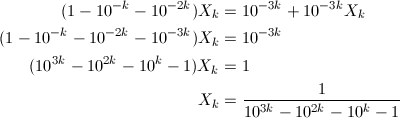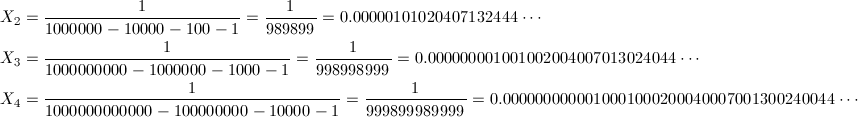小数点以下にフィボナッチ数列が出現する有理数

小数点以下に自然数

0以上の整数nを10^{k(n + 1)}で割って、n = 0から順に無限に足し合わせていった数X_kを考えます。kは1以上の整数ですが、例えば、k = 2だと、

$\begin{align*}X_2&=0.00 \\　&+0.0001 \\　&+0.000002 \\ &+0.00000003 \\ &+0.0000000004 \\ &\hspace{10mm}\vdots \\ &=0.00010203040506070809101112131415161718192021\cdots \end{align*}$

という数になります。この数は、小数点以下に自然数が順番に出現しますが、k桁ずつずらして足し合わせているだけなので、容易に想像できるように、順番にきれいに出現する自然数はk桁のものまでです。例えば、k = 1では、0.01234567901…となってしまいます。

一つ注意しなければならないのは、自然数をただ順番に並べていったチャンパーノウン定数（0.12345678910111213…）とは異なるということです。こちらは桁数に関係なく全ての数を重ならないように並べています。なお、チャンパーノウン定数は無理数でしかも超越数ですが、これから考える数は有理数（すなわち循環小数）になります。

まずは、前述の定義を数式で表してみます。

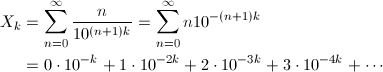
$\begin{align*} X_k&=\sum_{n=0}^\infty \frac{n}{10^{(n+1)k}}=\sum_{n=0}^\infty n10^{-(n+1)k} \\ &=0\cdot10^{-k}+1\cdot10^{-2k}+2\cdot10^{-3k}+3\cdot10^{-4k}+\cdots \end{align*}$

ここで、X_k - 10^{-k}X_kを計算します。

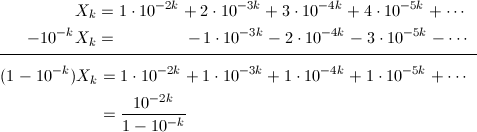
$\begin{align*} X_k&=1\cdot10^{-2k}+2\cdot10^{-3k}+3\cdot10^{-4k}+4\cdot10^{-5k}+\cdots \\ -10^{-k}X_k&=\hspace{16mm}-\hspace{0.5mm}1\cdot10^{-3k}-2\cdot10^{-4k}-3\cdot10^{-5k}-\cdots \end{align*} \vspace{-3mm} \\ \vspace{-3mm}\rule{110mm}{0.1mm} \\ \begin{align*} (1-10^{-k})X_k&=1\cdot10^{-2k}+1\cdot10^{-3k}+1\cdot10^{-4k}+1\cdot10^{-5k}+\cdots \\ &=\frac{10^{-2k}}{1-10^{-k}} \end{align*}$

単純な等比数列になりました。あとは式を整理すれば、

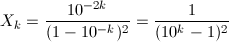
$X_k=\frac{10^{-2k}}{(1-10^{-k})^2}=\frac{1}{(10^k-1)^2}$

となり、シンプルな一般式が得られました。k = 2, 3, 4を計算してみると、

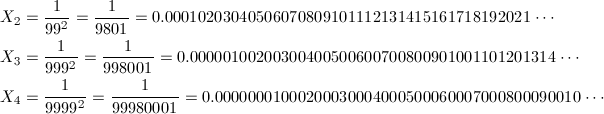
$\begin{align*} X_2&=\frac{1}{99^2}=\frac{1}{9801}=0.00010203040506070809101112131415161718192021\cdots \\ X_3&=\frac{1}{999^2}=\frac{1}{998001}=0.00000100200300400500600700800901001101201314\cdots \\ X_4&=\frac{1}{9999^2}=\frac{1}{99980001}=0.00000001000200030004000500060007000800090010\cdots \end{align*}$

となり、確かに小数点以下に自然数が順番に出現しています。なお、X_1は1/81 = 0.012345679…となりますが、前述の通り、小数点以下9桁目以降で隣の数字と桁が重なってしまい、自然数が順番に出現するという規則性は終わってしまいます。1/81は循環節が9桁の循環小数です。

小数点以下にフィボナッチ数列

次は、小数点以下に自然数ではなくフィボナッチ数列F_nが出現する数を考えてみます。フィボナッチ数列とは、次の規則によって得られる数列です。

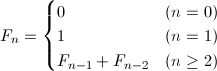
$F_n= \begin{cases} 0&(n=0) \\ 1&(n=1) \\ F_{n-1}+F_{n-2}&(n\ge2) \end{cases}$

具体的には、0、1、1、2、3、5、8、13、21、34、55、89、144、…となります。小数点以下にフィボナッチ数列が出現する数X_kを数式で表すと次のようになります。

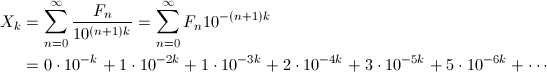
$\begin{align*} X_k&=\sum_{n=0}^\infty \frac{F_n}{10^{(n+1)k}}=\sum_{n=0}^\infty F_n10^{-(n+1)k} \\ &=0\cdot10^{-k}+1\cdot10^{-2k}+1\cdot10^{-3k}+2\cdot10^{-4k}+3\cdot10^{-5k}+5\cdot10^{-6k}+\cdots \end{align*}$

先ほどと同様に、X_k - 10^{-k}X_kを計算してみます。

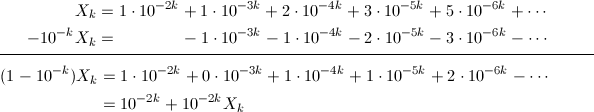
$\begin{align*} X_k&=1\cdot10^{-2k}+1\cdot10^{-3k}+2\cdot10^{-4k}+3\cdot10^{-5k}+5\cdot10^{-6k}+\cdots \\ -10^{-k}X_k&=\hspace{15mm}-\hspace{1mm}1\cdot10^{-3k}-1\cdot10^{-4k}-2\cdot10^{-5k}-3\cdot10^{-6k}-\cdots \end{align*} \vspace{-3mm} \\ \vspace{-3mm}\rule{\textwidth}{0.1mm} \\ \begin{align*} (1-10^{-k})X_k&=1\cdot10^{-2k}+0\cdot10^{-3k}+1\cdot10^{-4k}+1\cdot10^{-5k}+2\cdot10^{-6k}-\cdots \\ &=10^{-2k}+10^{-2k}X_k \end{align*}$

すると、右辺ではフィボナッチ数列の1つ前の項との差が取られていきますが、これはフィボナッチ数列の2つ前の項の値に他なりません。つまり、右辺の第2項目以降は、X_kを使って表すことができ、X_kに関する方程式となりました。あとは式を整理して、X_kについて解けば、

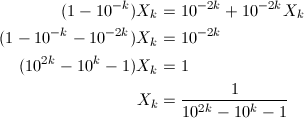
$\begin{align*} (1-10^{-k})X_k&=10^{-2k}+10^{-2k}X_k \\ (1-10^{-k}-10^{-2k})X_k&=10^{-2k} \\ (10^{2k}-10^k-1)X_k&=1 \\ X_k&=\frac{1}{10^{2k}-10^k-1} \end{align*}$

となり、一般式が得られました。k = 2, 3, 4を計算してみると、

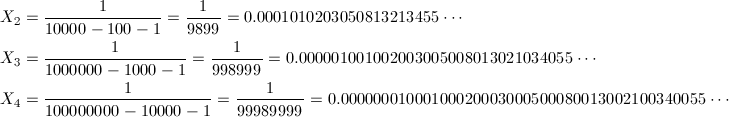
$\begin{align*} X_2&=\frac{1}{10000-100-1}=\frac{1}{9899}=0.0001010203050813213455\cdots \\ X_3&=\frac{1}{1000000-1000-1}=\frac{1}{998999}=0.000001001002003005008013021034055\cdots \\ X_4&=\frac{1}{100000000-10000-1}=\frac{1}{99989999}=0.00000001000100020003000500080013002100340055\cdots \end{align*}$

となります。なお、X_1は1/89=0.011235…ですが、こちらも小数点以下すぐに規則性が見えなくなってしまいます。とはいえ、「フィボナッチ数列の各項を1桁ずつずらして無限に足し合わせた数」が1/89というシンプルな有理数だった、というのは注目すべき事実ではありますね。また、奇しくも89はフィボナッチ数列に含まれる数でもあります。

小数点以下にトリボナッチ数列

最後はもう一歩進んで、小数点以下にトリボナッチ数列T_nが出現する数を考えてみます。トリボナッチ数列とは、フィボナッチ数列の考えを拡張したもので、次の規則によって得られる数列です。

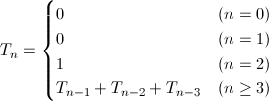
$T_n= \begin{cases} 0&(n=0) \\ 0&(n=1) \\ 1&(n=2) \\ T_{n-1}+T_{n-2}+T_{n-3}&(n\ge3) \end{cases}$

つまり、フィボナッチ数列が直前の2項を足し合わせていくのに対して、直前の3項を足し合わせていったものがトリボナッチ数列です。具体的には、0、0、1、1、2、4、7、13、24、44、…となります。小数点以下にトリボナッチ数列が出現する数を数式で表すと次のようになります。

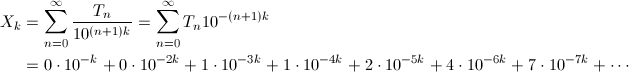
$\begin{align*} X_k&=\sum_{n=0}^\infty \frac{T_n}{10^{(n+1)k}}=\sum_{n=0}^\infty T_n10^{-(n+1)k} \\ &=0\cdot10^{-k}+0\cdot10^{-2k}+1\cdot10^{-3k}+1\cdot10^{-4k}+2\cdot10^{-5k}+4\cdot10^{-6k}+7\cdot10^{-7k}+\cdots \end{align*}$

ここで、今度は、X_k - 10^{-k}X_k - 10^{-2k}X_kを計算してみます。

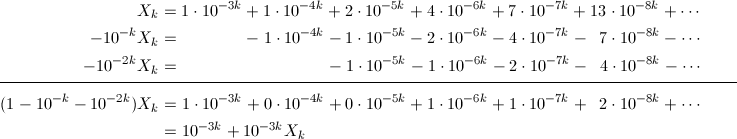
$\begin{align*} X_k&=1\cdot10^{-3k}+1\cdot10^{-4k}+2\cdot10^{-5k}+4\cdot10^{-6k}+7\cdot10^{-7k}+13\cdot10^{-8k}+\cdots \\ -10^{-k}X_k&=\hspace{15mm}-\hspace{1mm}1\cdot10^{-4k}-1\cdot10^{-5k}-2\cdot10^{-6k}-4\cdot10^{-7k}-\hspace{2mm}7\cdot10^{-8k}-\cdots \\ \hspace{13mm}-10^{-2k}X_k&=\hspace{34mm}-\hspace{1mm}1\cdot10^{-5k}-1\cdot10^{-6k}-2\cdot10^{-7k}-\hspace{2mm}4\cdot10^{-8k}-\cdots \end{align*} \vspace{-3mm} \\ \vspace{-3mm}\rule{170mm}{0.1mm} \\ \begin{align*} (1-10^{-k}-10^{-2k})X_k&=1\cdot10^{-3k}+0\cdot10^{-4k}+0\cdot10^{-5k}+1\cdot10^{-6k}+1\cdot10^{-7k}+\hspace{2mm}2\cdot10^{-8k}+\cdots \\ &=10^{-3k}+10^{-3k}X_k \end{align*}$

右辺では、トリボナッチ数列の1つ前の項と2つ前の項が引かれていきますが、これはトリボナッチ数列の3つ前の項の値と等しくなりますね。つまり、これまでと同様、右辺の第2項目以降をX_kで表すことができ、X_kに関する方程式が得られます。これをX_kについて解けば、

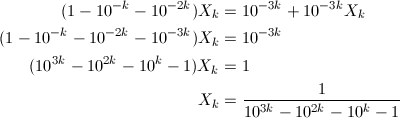
$\begin{align*} (1-10^{-k}-10^{-2k})X_k&=10^{-3k}+10^{-3k}X_k \\ (1-10^{-k}-10^{-2k}-10^{-3k})X_k&=10^{-3k} \\ (10^{3k}-10^{2k}-10^k-1)X_k&=1 \\ X_k&=\frac{1}{10^{3k}-10^{2k}-10^k-1} \end{align*}$

となり、一般式が得られました。k = 2, 3, 4を計算してみると、

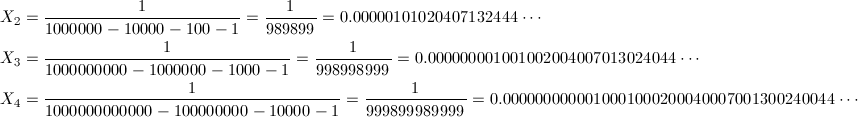
$\begin{align*} X_2&=\frac{1}{1000000-10000-100-1}=\frac{1}{989899}=0.00000101020407132444\cdots \\ X_3&=\frac{1}{1000000000-1000000-1000-1}=\frac{1}{998998999}=0.000000001001002004007013024044\cdots \\ X_4&=\frac{1}{1000000000000-100000000-10000-1}=\frac{1}{999899989999}=0.0000000000010001000200040007001300240044\cdots \end{align*}$

となります。なお、X_1は1/889=0.001124…です。

直前の2項を足したフィボナッチ数列、3項を足したトリボナッチ数列ときて、4項を足したものはテトラナッチ数列、5項を足したものはペンタナッチ数列、以降ヘキサナッチ数列、ヘプタナッチ数列というものが存在します。上記のフィボナッチ数列とトリボナッチ数列の結果を見ると、以降の一般式も想像できそうです。

小数点以下にフィボナッチ数列が出現する有理数

小数点以下に自然数

小数点以下にフィボナッチ数列

小数点以下にトリボナッチ数列

更新履歴