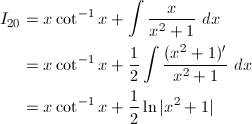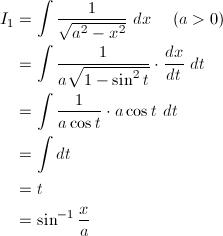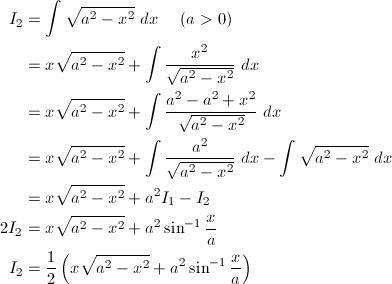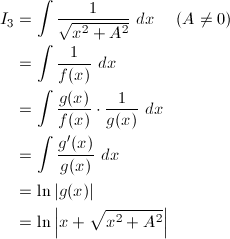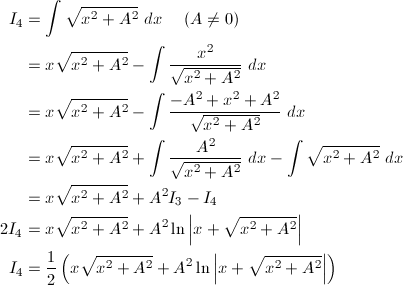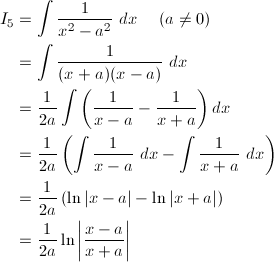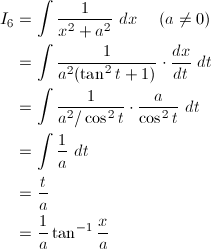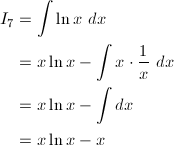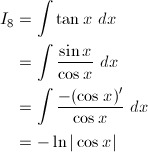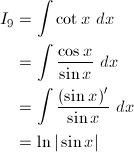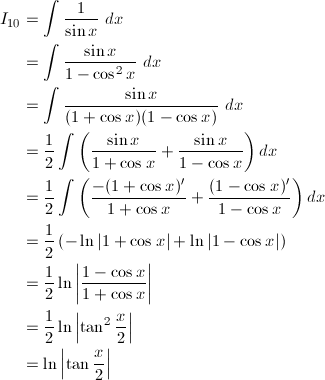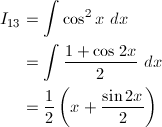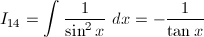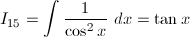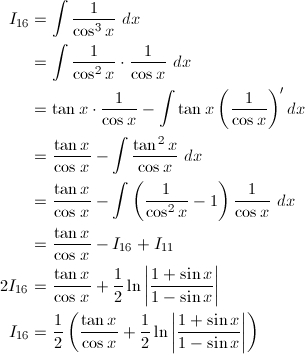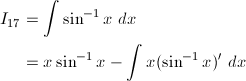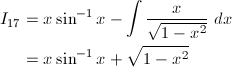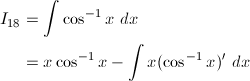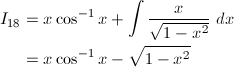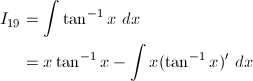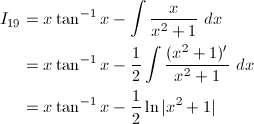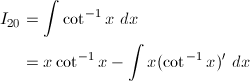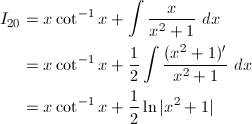不定積分20選（グラフ付き）

概要

私は、数学は好きなのですが、どういうわけか、積分だけは大嫌いです。大学レベルの積分でも苦戦してしまうほど苦手なので、よく見かける基本的な関数の不定積分の解法をここにメモしておきます。答えは一応教科書等で確認したので合っているはずです。

以下、不定積分の積分定数は全て省略しています。

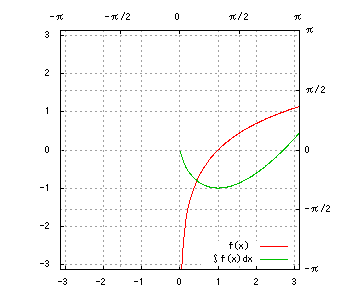
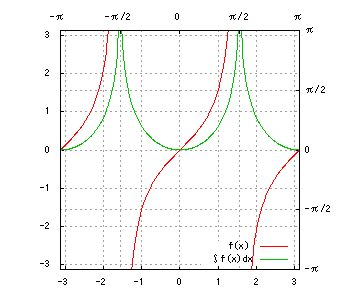
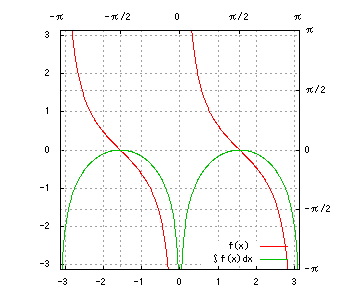
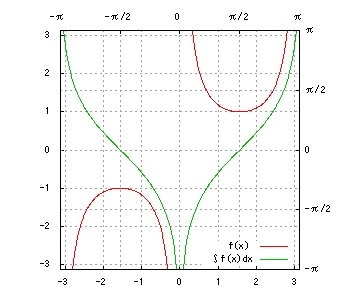
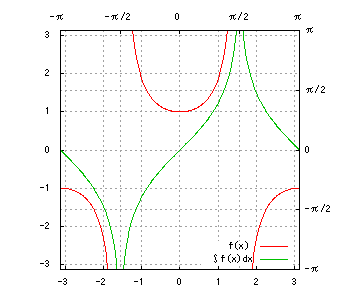
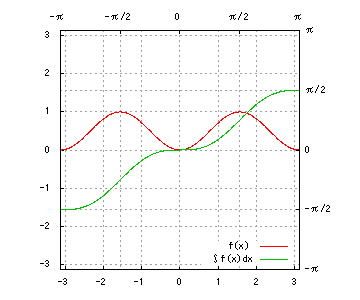
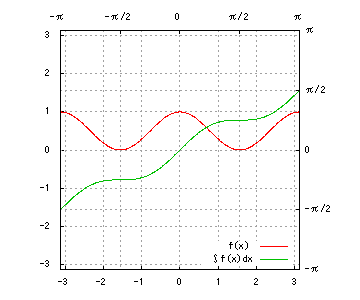
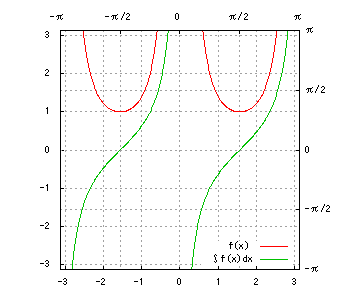
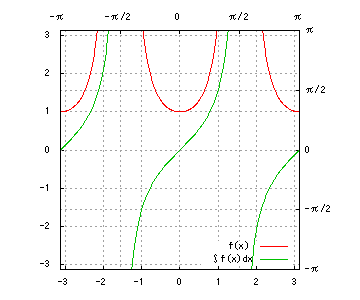
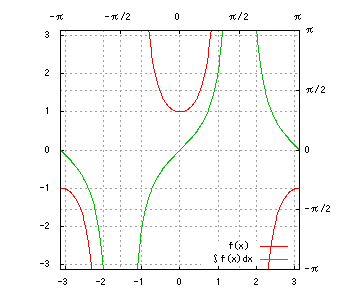
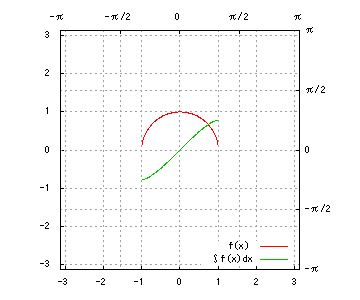
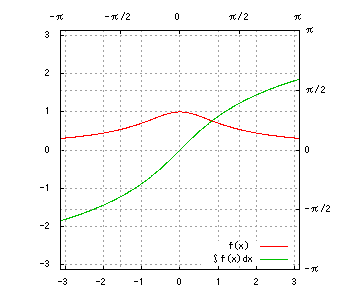
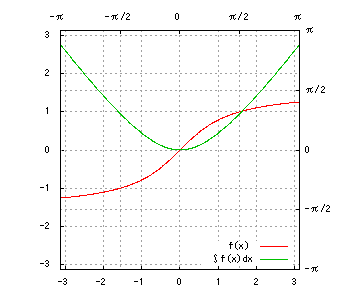
グラフは、赤が被積分関数、緑が不定積分です。赤を積分すると緑、緑を微分すると赤、です。積分定数は全て0です。

有理関数・無理関数

(1) 1 / √{a^2 - x^2}

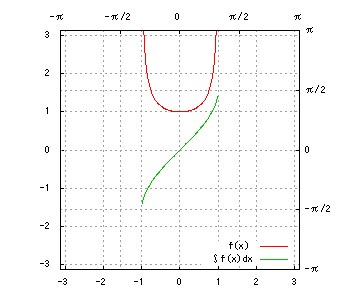
(1) a = 1

x = asintとおき、dx/dt = acostによって変数変換すると、

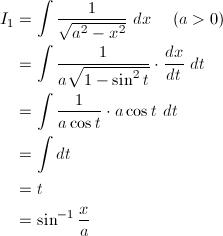
$\begin{align*} I_1&=\int\frac{1}{\sqrt{a^2-x^2}}\ dx \hspace{5mm}(a>0)\\ &=\int\frac{1}{a\sqrt{1-\sin^2t}}\cdot\frac{dx}{dt}\ dt\\ &=\int\frac{1}{a\cos t}\cdot a\cos t\ dt\\ &=\int dt\\ &=t\\ &=\sin^{-1}\frac{x}{a} \end{align*}$

(2) √{a^2 - x^2}

(2) a = 1

部分積分により、

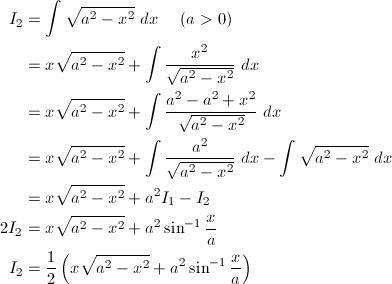
$\begin{align*} I_2&=\int\sqrt{a^2-x^2}\ dx\hspace{5mm}(a>0)\\ &=x\sqrt{a^2-x^2}+\int\frac{x^2}{\sqrt{a^2-x^2}}\ dx\\ &=x\sqrt{a^2-x^2}+\int\frac{a^2-a^2+x^2}{\sqrt{a^2-x^2}}\ dx\\ &=x\sqrt{a^2-x^2}+\int\frac{a^2}{\sqrt{a^2-x^2}}\ dx-\int\sqrt{a^2-x^2}\ dx\\ &=x\sqrt{a^2-x^2}+a^2I_1-I_2\\ 2I_2&=x\sqrt{a^2-x^2}+a^2\sin^{-1}\frac{x}{a}\\ I_2&=\frac{1}{2}\left(x\sqrt{a^2-x^2}+a^2\sin^{-1}\frac{x}{a}\right) \end{align*}$

(3) 1 / √{x^2 + A^2}

(3) A = 1

f(x) = √{x^2 + A^2}、g(x) = x + f(x)とすると、f'(x) = x / f(x)、g'(x) = 1 + x / f(x) = (f(x) + x) / f(x) = g(x) / f(x)なので、

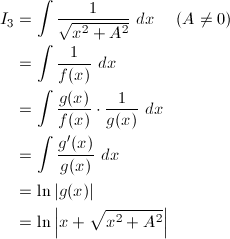
$\begin{align*} I_3&=\int\frac{1}{\sqrt{x^2+A^2}}\ dx\hspace{5mm}(A\ne0)\\ &=\int\frac{1}{f(x)}\ dx\\ &=\int\frac{g(x)}{f(x)}\cdot\frac{1}{g(x)}\ dx\\ &=\int\frac{g'(x)}{g(x)}\ dx\\ &=\ln|g(x)|\\ &=\ln\left|x+\sqrt{x^2+A^2}\right| \end{align*}$

(4) √{x^2 + A^2}

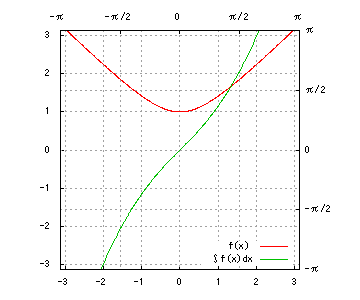
(4) A = 1

部分積分により、

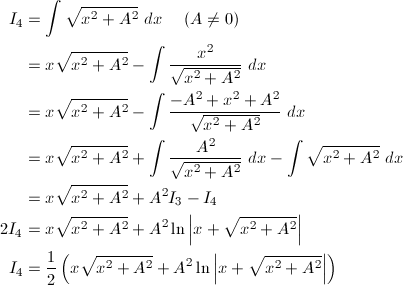
$\begin{align*} I_4&=\int\sqrt{x^2+A^2}\ dx\hspace{5mm}(A\ne0)\\ &=x\sqrt{x^2+A^2}-\int\frac{x^2}{\sqrt{x^2+A^2}}\ dx\\ &=x\sqrt{x^2+A^2}-\int\frac{-A^2+x^2+A^2}{\sqrt{x^2+A^2}}\ dx\\ &=x\sqrt{x^2+A^2}+\int\frac{A^2}{\sqrt{x^2+A^2}}\ dx-\int\sqrt{x^2+A^2}\ dx\\ &=x\sqrt{x^2+A^2}+A^2I_3-I_4\\ 2I_4&=x\sqrt{x^2+A^2}+A^2\ln\left|x+\sqrt{x^2+A^2}\right|\\ I_4&=\frac{1}{2}\left(x\sqrt{x^2+A^2}+A^2\ln\left|x+\sqrt{x^2+A^2}\right|\right) \end{align*}$

(5) 1 / (x^2 - a^2)

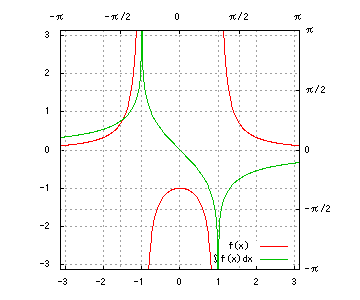
(5) a = 1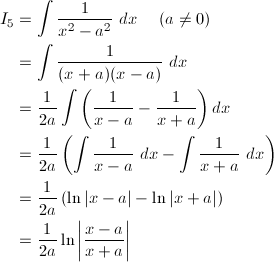

$\begin{align*} I_5&=\int\frac{1}{x^2-a^2}\ dx\hspace{5mm}(a\ne0)\\ &=\int\frac{1}{(x+a)(x-a)}\ dx\\ &=\frac{1}{2a}\int\left(\frac{1}{x-a}-\frac{1}{x+a}\right)dx\\ &=\frac{1}{2a}\left(\int\frac{1}{x-a}\ dx-\int\frac{1}{x+a}\ dx\right)\\ &=\frac{1}{2a}\left(\ln|x-a|-\ln|x+a|\right)\\ &=\frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right| \end{align*}$

(6) 1 / (x^2 + a^2)

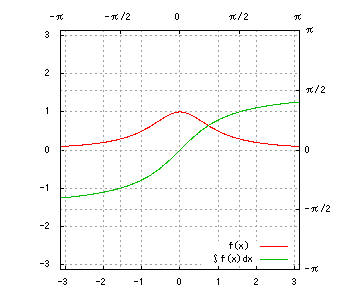
(6) a = 1

x = atantとおき、dx/dt = a / cos^2tによって変数変換すると、

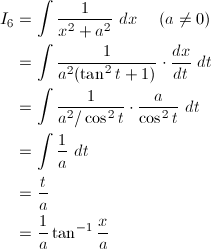
$\begin{align*} I_6&=\int\frac{1}{x^2+a^2}\ dx\hspace{5mm}(a\ne0)\\ &=\int\frac{1}{a^2(\tan^2t+1)}\cdot\frac{dx}{dt}\ dt\\ &=\int\frac{1}{a^2/\cos^2t}\cdot\frac{a}{\cos^2t}\ dt\\ &=\int\frac{1}{a}\ dt\\ &=\frac{t}{a}\\ &=\frac{1}{a}\tan^{-1}\frac{x}{a} \end{align*}$

対数関数

(7) lnx

(7)

部分積分により、

$\begin{align*} I_7&=\int\ln x\ dx\\ &=x\ln x-\int x\cdot\frac{1}{x}\ dx\\ &=x\ln x-\int dx\\ &=x\ln x-x \end{align*}$

三角関数

(8) tanx

(8)

$\begin{align*} I_8&=\int\tan x\ dx\\ &=\int\frac{\sin x}{\cos x}\ dx\\ &=\int\frac{-(\cos x)'}{\cos x}\ dx\\ &=-\ln|\cos x| \end{align*}$

(9) cotx

(9)

$\begin{align*} I_9&=\int\cot x\ dx\\ &=\int\frac{\cos x}{\sin x}\ dx\\ &=\int\frac{(\sin x)'}{\sin x}\ dx\\ &=\ln|\sin x| \end{align*}$

(10) 1 / sinx (= cscx)

(10)

$\begin{align*} I_{10}&=\int\frac{1}{\sin x}\ dx\\ &=\int\frac{\sin x}{1-\cos^2x}\ dx\\ &=\int\frac{\sin x}{(1+\cos x)(1-\cos x)}\ dx\\ &=\frac{1}{2}\int\left(\frac{\sin x}{1+\cos x}+\frac{\sin x}{1-\cos x}\right)dx\\ &=\frac{1}{2}\int\left(\frac{-(1+\cos x)'}{1+\cos x}+\frac{(1-\cos x)'}{1-\cos x}\right)dx\\ &=\frac{1}{2}\left(-\ln|1+\cos x|+\ln|1-\cos x|\right)\\ &=\frac{1}{2}\ln\left|\frac{1-\cos x}{1+\cos x}\right|\\ &=\frac{1}{2}\ln\left|\tan^2\frac{x}{2}\right|\\ &=\ln\left|\tan\frac{x}{2}\right| \end{align*}$

(11) 1 / cosx (= secx)

(11)

$\begin{align*} I_{11}&=\int\frac{1}{\cos x}\ dx\\ &=\int\frac{\cos x}{1-\sin^2x}\ dx\\ &=\int\frac{\cos x}{(1+\sin x)(1-\sin x)}\ dx\\ &=\frac{1}{2}\int\left(\frac{\cos x}{1+\sin x}+\frac{\cos x}{1-\sin x}\right)dx\\ &=\frac{1}{2}\int\left(\frac{(1+\sin x)'}{1+\sin x}-\frac{(1-\sin x)'}{1-\sin x}\right)dx\\ &=\frac{1}{2}\left(\ln|1+\sin x|-\ln|1-\sin x|\right)\\ &=\frac{1}{2}\ln\left|\frac{1+\sin x}{1-\sin x}\right| \end{align*}$

三角関数の累乗

(12) sin^2x

(12)

$\begin{align*} I_{12}&=\int\sin^2x\ dx\\ &=\int\frac{1-\cos2x}{2}\ dx\\ &=\frac{1}{2}\left(x-\frac{\sin2x}{2}\right) \end{align*}$

(13) cos^2x

(13)

$\begin{align*} I_{13}&=\int\cos^2x\ dx\\ &=\int\frac{1+\cos2x}{2}\ dx\\ &=\frac{1}{2}\left(x+\frac{\sin2x}{2}\right) \end{align*}$

(14) 1 / sin^2x (= csc^2x)

(14)

(1 / tanx)' = -1 / sin^2xなので、

$\begin{align*} I_{14}&=\int\frac{1}{\sin^2x}\ dx=-\frac{1}{\tan x} \end{align*}$

(15) 1 / cos^2x (= sec^2x)

(15)

(tanx)' = 1 / cos^2xなので、

$\begin{align*} I_{15}&=\int\frac{1}{\cos^2x}\ dx=\tan x \end{align*}$

(16) 1 / cos^3x (= sec^3x)

(16)

部分積分により、

$\begin{align*} I_{16}&=\int\frac{1}{\cos^3x}\ dx\\ &=\int\frac{1}{\cos^2x}\cdot\frac{1}{\cos x}\ dx\\ &=\tan x\cdot\frac{1}{\cos x}-\int\tan x\left(\frac{1}{\cos x}\right)'dx\\ &=\frac{\tan x}{\cos x}-\int\frac{\tan^2x}{\cos x}\ dx\\ &=\frac{\tan x}{\cos x}-\int\left(\frac{1}{\cos^2x}-1\right)\frac{1}{\cos x}\ dx\\ &=\frac{\tan x}{\cos x}-I_{16}+I_{11}\\ 2I_{16}&=\frac{\tan x}{\cos x}+\frac{1}{2}\ln\left|\frac{1+\sin x}{1-\sin x}\right|\\ I_{16}&=\frac{1}{2}\left(\frac{\tan x}{\cos x}+\frac{1}{2}\ln\left|\frac{1+\sin x}{1-\sin x}\right|\right) \end{align*}$

逆三角関数

(17) sin^{-1}x

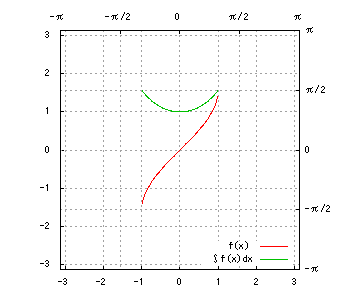
(17)

部分積分により、

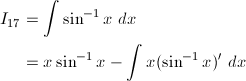
$\begin{align*} I_{17}&=\int\sin^{-1}x\ dx\\ &=x\sin^{-1}x-\int x(\sin^{-1}x)'\ dx \end{align*}$

I_1の結果を用いて、

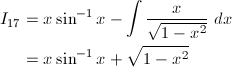
$\begin{align*} I_{17}&=x\sin^{-1}x-\int\frac{x}{\sqrt{1-x^2}}\ dx\\ &=x\sin^{-1}x+\sqrt{1-x^2} \end{align*}$

(18) cos^{-1}x

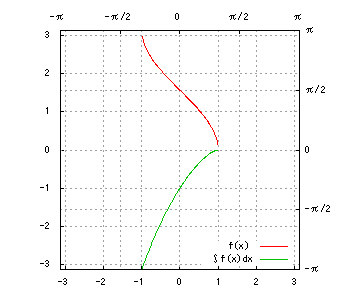
(18)

部分積分により、

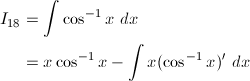
$\begin{align*} I_{18}&=\int\cos^{-1}x\ dx\\ &=x\cos^{-1}x-\int x(\cos^{-1}x)'\ dx \end{align*}$

y = cos^{-1}xとおくと、y' = -1 / siny = -1 / √{1 - cos^2y} = -1 / √{1 - x^2}なので、

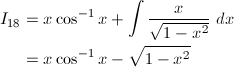
$\begin{align*} I_{18}&=x\cos^{-1}x+\int\frac{x}{\sqrt{1-x^2}}\ dx\\ &=x\cos^{-1}x-\sqrt{1-x^2} \end{align*}$

(19) tan^{-1}x

(19)

部分積分により、

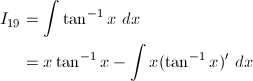
$\begin{align*} I_{19}&=\int\tan^{-1}x\ dx\\ &=x\tan^{-1}x-\int x(\tan^{-1}x)'\ dx \end{align*}$

I_6の結果を用いて、

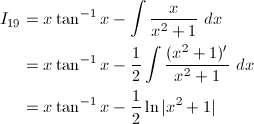
$\begin{align*} I_{19}&=x\tan^{-1}x-\int\frac{x}{x^2+1}\ dx\\ &=x\tan^{-1}x-\frac{1}{2}\int\frac{(x^2+1)'}{x^2+1}\ dx\\ &=x\tan^{-1}x-\frac{1}{2}\ln|x^2+1| \end{align*}$

(20) cot^{-1}x

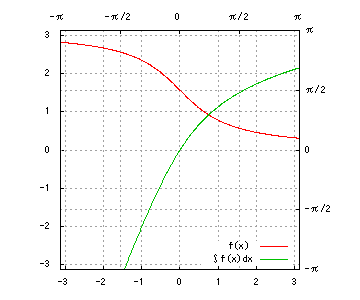
(20)

部分積分により、

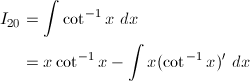
$\begin{align*} I_{20}&=\int\cot^{-1}x\ dx\\ &=x\cot^{-1}x-\int x(\cot^{-1}x)'\ dx \end{align*}$

y = cot^{-1}xとおくと、y' = 1 / (coty)' = 1 / (-1 / sin^2y) = -1 / (cot^2y + 1) = -1 / (x^2 + 1)なので、

$\begin{align*} I_{20}&=x\cot^{-1}x+\int\frac{x}{x^2+1}\ dx\\ &=x\cot^{-1}x+\frac{1}{2}\int\frac{(x^2+1)'}{x^2+1}\ dx\\ &=x\cot^{-1}x+\frac{1}{2}\ln|x^2+1| \end{align*}$

不定積分20選（グラフ付き）

概要

有理関数・無理関数

(1) 1 / √{a^2 - x^2}

(2) √{a^2 - x^2}

(3) 1 / √{x^2 + A^2}

(4) √{x^2 + A^2}

(5) 1 / (x^2 - a^2)

(6) 1 / (x^2 + a^2)

対数関数

(7) lnx

三角関数

(8) tanx

(9) cotx

(10) 1 / sinx (= cscx)

(11) 1 / cosx (= secx)

三角関数の累乗

(12) sin^2x

(13) cos^2x

(14) 1 / sin^2x (= csc^2x)

(15) 1 / cos^2x (= sec^2x)

(16) 1 / cos^3x (= sec^3x)

逆三角関数

(17) sin^{-1}x

(18) cos^{-1}x

(19) tan^{-1}x

(20) cot^{-1}x

更新履歴