マンデルブロ集合を観察する
フラクタル図形であるマンデルブロ集合を観察してみましょう。その特徴を簡単に解説します。
フラクタル性
マンデルブロ集合はフラクタル図形です。フラクタルとは、簡単に言うと、拡大しても複雑さが変わらず、全体と似たような形が細部に存在するような図形(自己相似な図形)のことを言います。
フラクタルでない普通の図形の場合は、全体がいくら複雑な形をしていても、細かく拡大していけばいつかは平らな線や単純な形が見えてくるだろうと予想しますよね。ところが、フラクタル図形であるマンデルブロ集合は、その境界線をどんなに拡大しても決して平坦になることはありません。それどころか、拡大していくと全体像と似たような形が次々と現れます。当然、それらをまた拡大するとまた同じような形…と永遠に出会うことになるのです。
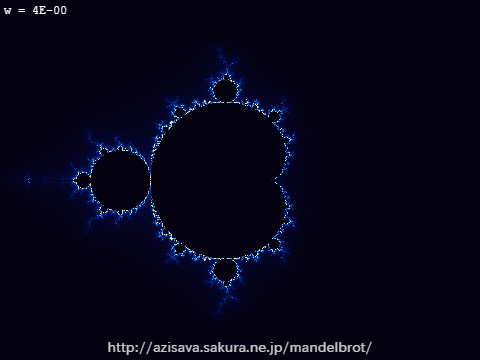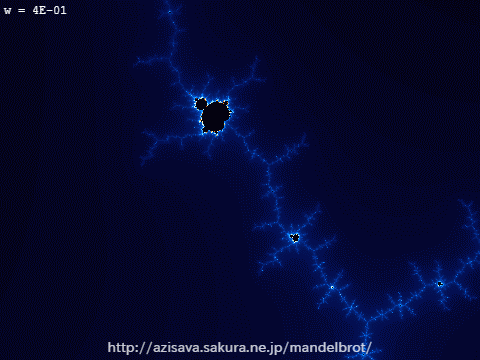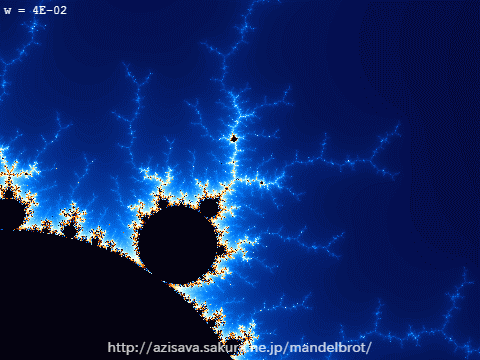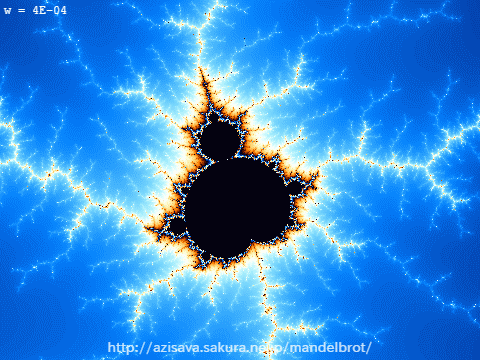
図3-1:1万倍に拡大しても複雑さが変わらず、最初と同じ形が散見される。
この先拡大し続けても決して平らな線が現れることはない。
実は、マンデルブロ集合の境界線の長さは無限大と言われています(※1)。これは、拡大してそのスケールの定規で測定し直すといくらでも長く測定できてしまうということです。囲われている面積は有限なのに、不思議ですね。
ちなみに、マンデルブロ集合以外の有名で分かりやすいフラクタル図形としては、コッホ曲線やシェルピンスキーの三角形などが挙げられます。また、フラクタルは自然界にも存在し、陸地の海岸線や野菜のロマネスコなどはフラクタル的な造形をしています。
- ※1:これは証明されていますが、その証明の内容は難解ですのでここでは割愛させていただきます。興味がある方は専門書や論文を参照してみて下さい。
マンデルブロ集合の構造
マンデルブロ集合の遠景を見ると、周囲にちぎれた“飛び地”のような部分が見られますが、拡大してみれば分かるように、これらは全て必ずつながっています(※2)。他にも、渦巻きのようだったり、放射状に伸びていたり、実に複雑でさまざまな形が見られますが、マンデルブロ集合には“穴”が開いていることもありません(※3)。つまり、トポロジー的にはただの円板と同じなのです。
マンデルブロ集合の大部分を占める中央の大きな特徴的なハート型はカージオイド(心臓形)と呼ばれる図形です。そしてその左(-3/4, 0)で接しているのは、中心が-1、半径が1/4の円です。そしてさらに、これらの周りにさらに無数の円が接しているように見えますが、実は最初の半径1/4の大きな円以外は全て、円に非常に近いものの円ではない図形であると言われています。つまり、拡大したときに見えてくる全体像と似た形は、完全な相似形ではなく、全て少しずつ異なっているのです。
このように、マンデルブロ集合は、中央の大きなカージオイドと円の周りに、小さなカージオイド(に似た図形)と円(に似た図形)のパーツが接し合ってできています。マンデルブロ集合とはで紹介しました数列の軌道を確認できるプログラムを見ていただくと分かりますが、実は、同じパーツの中からCを選ぶと、同じ周期の振動状態に収束します。特に、最も大きなカージオイドは周期1(1つの値に収束)、最も大きな円は周期2(2つの値の間の振動状態)に収束します。それ以外の小さな円はもっと大きな周期の振動状態に収束します。
- ※2、※3:これらは証明されていますが、その証明の内容は難解ですのでここでは割愛させていただきます。興味がある方は専門書や論文を参照してみて下さい。
特徴的なポイント
最も大きなカージオイドと左の円との間には“谷”があります。この部分は拡大すると、タツノオトシゴを連想させる模様がずらりと並んでいるため、Seahorse valley(タツノオトシゴの谷)などと呼ばれることがあります。また、最も大きなカージオイドの右側にも谷間がありますが、こちらには鼻を伸ばした象を連想させる模様がずらりと並んでいるため、Elephant valley(象の谷)などと呼ばれることがあります。
他にも拡大するとさまざまな特徴的な模様を見つけることができます。以下の番号をクリックするとその地点の拡大アニメーションが見られます。
- タツノオトシゴ(Seahorse valley)
- 鼻を伸ばした象(Elephant valley)
- ミニマンデルブロ集合
- 四葉のクローバー