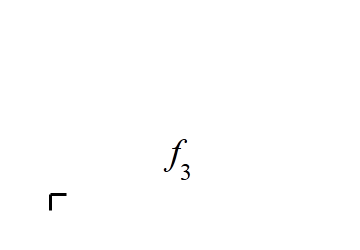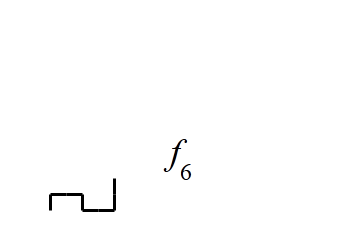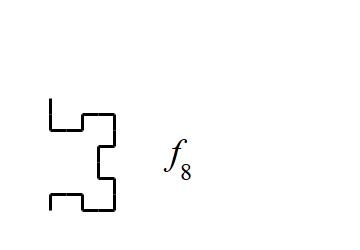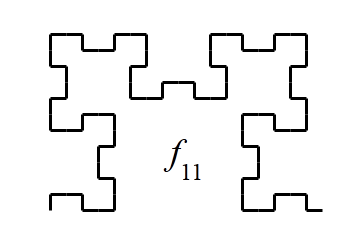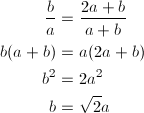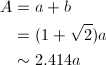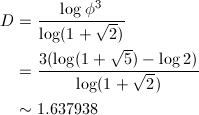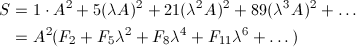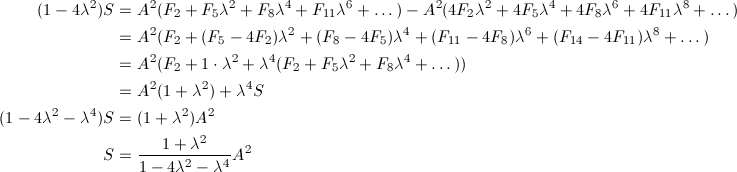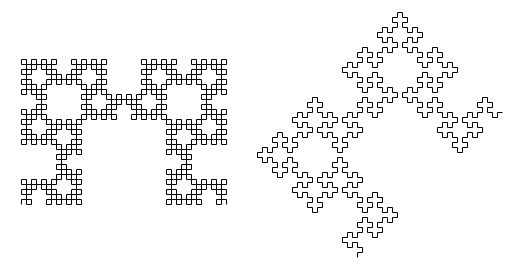フィボナッチ文字列フラクタル

フィボナッチ文字列とは

フィボナッチ文字列（Fibonacci word）、または、フィボナッチ列、フィボナッチワードとは、フィボナッチ数列の文字列版です。数を足していく代わりに、文字を連結していきます。すなわち、

S_1 = 1、S_2 = 0として、S_n = S_{n-1}S_{n-2}（文字列連結）によって生成されていく文字列S_n

をフィボナッチ文字列といいます。具体的には、次のようになります。

S_1 = 1
S_2 = 0
S_3 = 01
S_4 = 010
S_5 = 01001
S_6 = 01001010
S_7 = 0100101001001
    :
S_{∞} = 01001010010010100101001001010010010100101001001010010100100101001001010010100100101001001…

このように2種類の文字を使い、1つ前の文字列の後ろに2つ前の文字列をつなげて作られていきます。あるいは、次のような別の定義も存在します。

S_1 = 1として、1→0、0→01の変換によって作られる文字列S_n

これら2つの全く異なる定義が同一の文字列を生み出すことは、次のようにして説明できます。S_nは第1の定義よりS_{n-1}S_{n-2}ですが、仮に第2の定義の変換によってS_{n-1}→S_nとS_{n-2}→S_{n-1}が成り立つならば、S_{n-1}S_{n-2}はS_nS_{n-1}と変換され、これは第1の定義よりS_{n+1}に等しくなるため、S_n→S_{n+1}が成り立つことになります。S_1→S_2、および、S_2→S_3が成り立っていることは明らかなので、数学的帰納法により、全てのnについて両方の定義が等しい文字列を生み出していることが分かります。

フィボナッチ文字列の主な特徴は、次の通りです。

2文字以上の連続した1、および、3文字以上の連続した0は出現しない。
n ≥ 3では、最後の二文字は、nが奇数の場合01、偶数の場合10である。
n ≥ 4では、最後の二文字を取り去ると、回文になる。
フィボナッチ数列F_nをF_0 = 0, F_1 = 1, …とすると、S_nの文字数はF_n、S_nに含まれる0の数はF_{n-1}、n ≥ 2のS_nに含まれる1の数は、F_{n-2}に等しい。
フィボナッチ数列の隣接する2項の比が黄金比に収束することから、フィボナッチ文字列に含まれる0と1の数の比もn→∞で黄金比になる。

いずれの特徴も定義から比較的簡単に説明することができます。フィボナッチ文字列には、ここに挙げた他にも興味深い特徴が多く存在します。

フィボナッチ文字列フラクタルとは

フィボナッチ文字列フラクタル（Fibonacci word fractal）、または、フィボナッチ列フラクタル、フィボナッチワードフラクタルとは、フィボナッチ文字列に基づいて得られるフラクタル曲線です。フィボナッチ文字列S_nのk文字目に対して、次の規則を適用します。

表1-フィボナッチ文字列フラクタルを描く規則
S_nのk文字目	k	動作
0	kが奇数	現在の向きに1単位前進し、	90度右に向きを変える。
0	kが偶数		90度左に向きを変える。
1	問わない		向きは変えない。

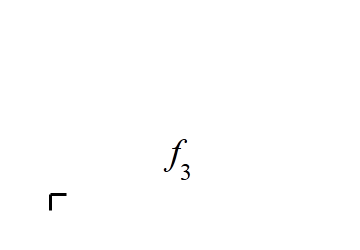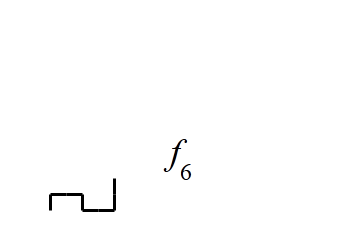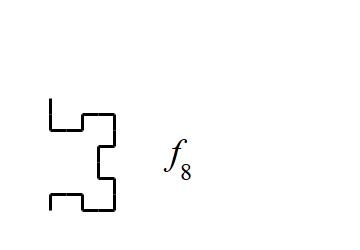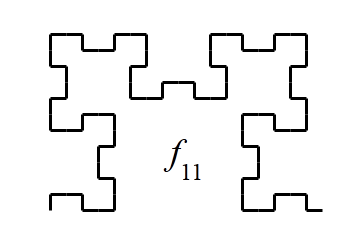
図1-f_3からf_{11}まで

この規則を、1文字目から最後の文字まで順にくり返して生成された曲線をf_nとし、n→∞としたものがフィボナッチ文字列フラクタルです。

例えば、S_6は01001010なので、f_6を描くには、上記規則に従い、前進→右を向く→前進→前進→右を向く→前進→左を向く→前進→前進→左を向く→前進→前進→左を向く、という作業を行えばよいのです。

図1には、f_3からf_{11}までの曲線を生成するようすを示しました。また、図2には、さらに高次のf_{23}を示しました。黒一色だと味気なかったので、左下の始点からの距離に応じて適当に色をつけてみました。ここまで来ると人の手で描くのは困難ですね。f_{11}に比べて、自己相似性・フラクタル性も顕著になっています。曲線の長さは、F_{23} = 28657単位、途中で曲がった回数は、F_{22} = 17711回におよびます。

以降の節では、このフィボナッチ文字列フラクタル曲線の特徴を紹介していきます。

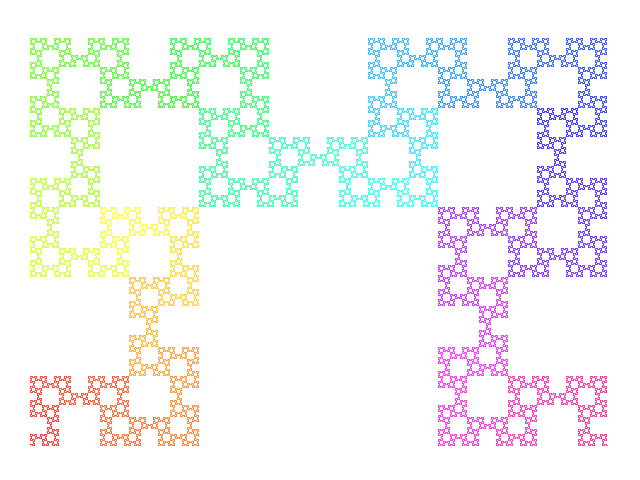
第23次のフィボナッチ文字列フラクタル曲線f23
図2-第23次のフィボナッチ文字列フラクタル曲線f_{23}

相似形が現れる周期

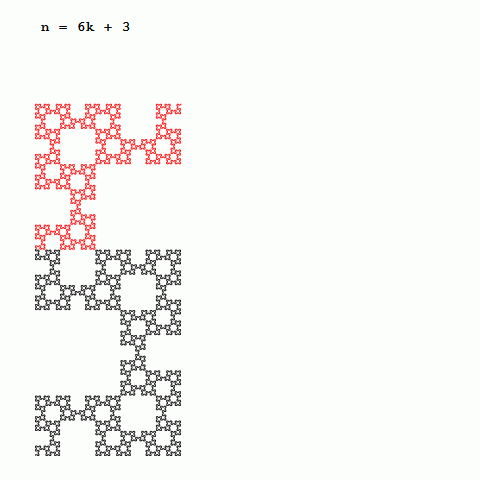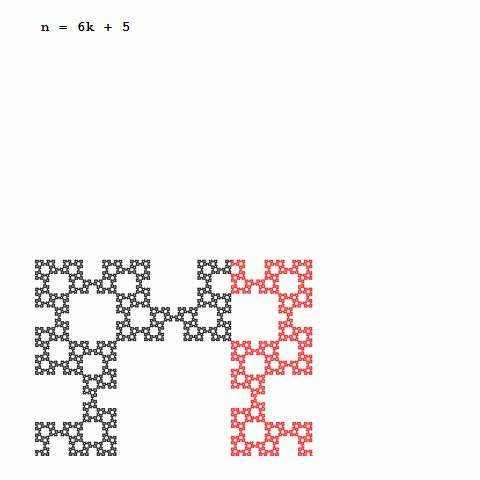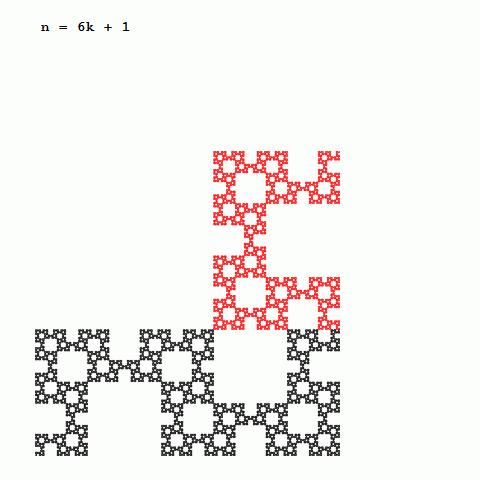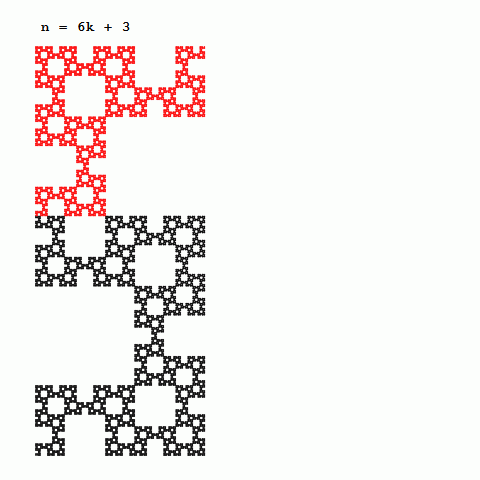
図3-nが6増えるごとに相似で向きも同じ形状が現れる

まずは、図3をご覧下さい。高次の曲線を観察すると、nが6増えるごとに形が相似で向きも同じ形状に出会うことが分かります。向きを考えないのであれば、nが3増えるごとに相似な形となっています。nを3で割った余りが、0の場合はＳ字型、1の場合はＬ字型、2の場合はコの字型をしています。また、新たに付け加わった部分は、2つ前のものと相似な形をしています。

nが3増えて相似な形が現れたとき、大きさは何倍になっているでしょうか？先ほどの図2を使って考えてみます。これはコの字型です。f_{23}の縦横の長さをA、Bとし、左下に見られる向きが90度回転した同じ形の部分（すなわちf_{20}だった部分）の縦横の長さをb、aとします。図を注意深く眺めれば、A = a + b、B = 2a + bであることがすぐ分かると思います。b/a = B/Aなので、

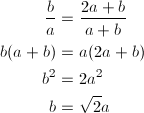
$\begin{align*} \frac{b}{a}&=\frac{2a+b}{a+b}\\ b(a+b)&=a(2a+b)\\ b^2&=2a^2\\ b&=\sqrt{2}a\\ \end{align*}$

となって、まずは縦横の比が1 : √{2}であることが分かります。そして、このbを用いると、

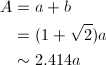
$\begin{align*} A&=a+b\\ &=(1+\sqrt{2})a\\ &\sim2.414a \end{align*}$

となるため、結局nが3増えるごとに、大きさは約2.414倍になっていることが分かります。ちなみに1 + √{2}という数は、白銀比と呼ばれることがあります。

なお、解説のために図2を使いましたが、以上が成り立つのは正確にはf_{∞}のみです。f_{23}の縦横の比は、実際には1：約1.41769です。

縦横の長さ

前節では、f_{∞}の曲線がコの字型になった場合について、縦横の比を考察しました。実は、n ≥ 3の場合、縦横の長さa_nとb_nについて6ステップごとに次の漸化式が成り立ちます。ここに、a_1 = a_2 = 1、b_1 = b_2 = 0です。

表2-縦横の長さが満たす漸化式と縦横の比の極限
n（kは自然数）	a_nの漸化式		b_nの漸化式		縦横の比の極限a_{∞} : b_{∞}	形状
6k	a_n =	a_{n-1} + 1	b_n =	b_{n-1} + a_{n-2}	1 : 1 + √{2}	Ｓ字型
6k + 1		a_{n-1} + b_{n-2}		b_{n-1}	1 : 1	Ｌ字型
6k + 2		a_{n-1} + a_{n-2}		b_{n-1}	√{2} : 1	コ字型
6k + 3		a_{n-1} + b_{n-2}		b_{n-1} + 1	1 + √{2} : 1	Ｓ字型
6k + 4		a_{n-1}		b_{n-1} + a_{n-2}	1 : 1	Ｌ字型
6k + 5		a_{n-1}		b_{n-1} + b_{n-2}	1 : √{2}	コ字型

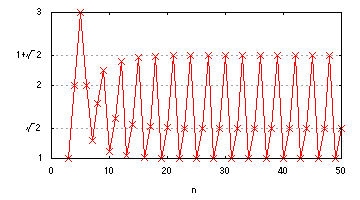
図4-短い辺に対する長い辺の比

漸化式の中で、+1というのは理解しにくいかもしれませんが、図1を見ていただけると、例えばf_9などでは、次の曲線に接続するため、右上に1単位分出っ張りがあるのが分かると思います。これが+1です。

これらの漸化式で十分大きなnまで縦横の長さを計算すると、6で割った余りに応じて、縦横の比が一定の極限値に至ることが分かります。ただし、表2の上の3つと下の3つはそれぞれ縦と横が逆転した形状になっているだけなので、向きを考えないのであれば、比は3種類になります。図4には、短い辺に対する長い辺の比が1、√{2}、1 + √{2}の3種類に収束する様子をグラフにしました。

なお、これらの結果は、前節のように、f_{∞}の図を眺めて式を立てることによっても同じように得られます。

フラクタル次元

フラクタル次元（fractal dimension）とは、フラクタル図形の複雑さを表す指標の一つです。2次元の面は1次元の線を無限に緻密に並べたもの、あるいは1次元の線は2次元の面を無限に細く刻んだものと考えると、曲線によるフラクタル図形は、無限に緻密であるが面と呼ぶには十分でない、1次元と2次元の中間のような性質があると言えます。この性質を数値化したものがフラクタル次元です。

最もよく用いられるフラクタル次元の定義は、次の通りです。その図形を1/Nに縮小したものをM個集めると元の図形になるとき、D = logM / logNをフラクタル次元とします。例えば、通常の正方形は、各辺を1/2に縮小したものを4つ集めると元の正方形になるため、log4 / log2 = 2次元の図形です。

しかし、フィボナッチ文字列フラクタルにこの定義を適用するには、少し工夫が必要です。まず、1 / (1 + √{2})倍にすると、3ステップ前の相似な図形となることは、すでに述べた通りです。でも、これをいくつ集めれば元の図形になるかというと、図を見ても単純には求められません。

そこで、曲線f_nの長さがフィボナッチ数F_nに等しかったことを思い出して下さい。フィボナッチ数の隣接する2項の比が黄金比φ = (1 + √{5}) / 2になるため、1ステップで曲線の長さはφ倍になっているのです。1 / (1 + √{2})倍すると、3ステップ前に戻るため、これをφ^3個集めれば、元に戻ると考えることができます。したがって、フィボナッチ文字列フラクタルのフラクタル次元は、

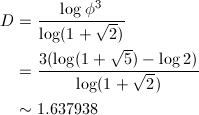
$\begin{align*} D&=\frac{\log\phi^3}{\log(1+\sqrt{2})}\\ &=\frac{3(\log(1+\sqrt{5})-\log2)}{\log(1+\sqrt{2})}\\ &\sim 1.637938 \end{align*}$

と求められます。この通り、フラクタルな曲線のフラクタル次元は整数になりません。まさに線と面の中間の性質を持っていると言えます。

正方形の穴

高次のフィボナッチ文字列フラクタルを眺めてみると、大小の正方形の穴が見えますね。この穴にはどのような特徴があるでしょうか。

図5-長方形に穴をあけていくことでフィボナッチ文字列フラクタルができる様子

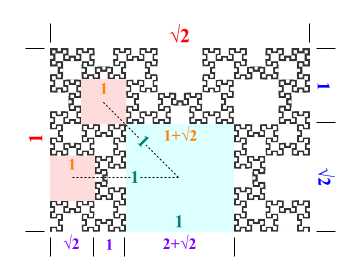
図6-正方形の大きさと正方形同士の距離

図7-正方形の穴の大きさごとの個数

まず、大きい穴ほど少なく、小さい穴ほど無数にあります。あるサイズの穴の周囲8方向には、一回り小さいサイズの穴がきれいに並ぶように配置しています。サイズが一段階異なる穴は、3ステップずれた相似形の一部となっているため、大きさの比は1 + √{2}倍であることがすぐ分かります。さらに、図6のような各辺の比をもとに計算すると、正方形の一辺の長さと、その正方形の中心と周囲に配置している一回り小さい正方形の中心との距離は、全て等しいことが分かります。

さらに特筆すべきなのは、同じ大きさの穴の個数です。なんと、全てフィボナッチ数になっています。Ｓ字型はF_{3k}、Ｌ字型はF_{3k+1}、コ字型はF_{3k+2}のフィボナッチ数が登場します。例えば、図7のように、コの字型の正方形の穴の数を大きいサイズのものから数えてみると、1個、5個、21個、89個、…となっており、2番目、5番目、8番目、11番目、…のフィボナッチ数に等しくなっています。

ところで、図5のアニメーションを見るとすぐに分かる通り、1 : √{2}の長方形にこの正方形の穴を適切な位置に次々に無限にあけていくと、これまで見てきたものと同じフィボナッチ文字列フラクタルが得られます。先ほどこのフラクタル図形のフラクタル次元が1と2の中間の値になることを示しましたが、これはつまり線が緻密になって面に近づいたものであると同時に、面が疎らになって線に近づいたものでもあるのです。

実際にこの調子で無限個の正方形の穴をあけていくと、面積はどうなるでしょうか。

コの字型の場合で考えてみます。最初の長方形の大きさをa × √{2}aとします。すると、一番大きい正方形の穴の一辺の長さAは、図6より、A = √{2}a / (1 + √{2}) = (2 - √{2})aとなります。正方形の大きさは、一段階ごとに1 / (1 + √{2}) = √{2} - 1倍になっていくので、これをλとおくと、無限個の穴の面積の合計Sは、

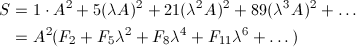
$\begin{align*} S&=1\cdot A^2+5(\lambda A)^2+21(\lambda^2A)^2+89(\lambda^3A)^2+\dots\\ &=A^2(F_2+F_5\lambda^2+F_8\lambda^4+F_{11}\lambda^6+\dots)\\ \end{align*}$

となります。3項離れたフィボナッチ数の間には、F_n = 4F_{n-3} + F_{n-6}という関係があるので、ここでS - 4λ^2Sを計算してみると、

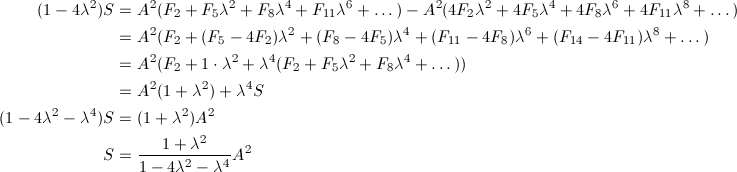
$\begin{align*} (1-4\lambda^2)S&=A^2(F_2+F_5\lambda^2+F_8\lambda^4+F_{11}\lambda^6+\dots)-A^2(4F_2\lambda^2+4F_5\lambda^4+4F_8\lambda^6+4F_{11}\lambda^8+\dots)\\ &=A^2(F_2+(F_5-4F_2)\lambda^2+(F_8-4F_5)\lambda^4+(F_{11}-4F_8)\lambda^6+(F_{14}-4F_{11})\lambda^8+\dots)\\ &=A^2(F_2+1\cdot\lambda^2+\lambda^4(F_2+F_5\lambda^2+F_8\lambda^4+\dots))\\ &=A^2(1+\lambda^2)+\lambda^4S\\ (1-4\lambda^2-\lambda^4)S&=(1+\lambda^2)A^2\\ S&=\frac{1+\lambda^2}{1-4\lambda^2-\lambda^4}A^2 \end{align*}$

となり、Sが求められます。λ = √{2} - 1およびA = (2 - √{2})aを代入すると、最終的にS = √{2}a^2となり、最初の長方形の面積に等しくなります。すなわち、無限個の穴をあけると、面積は0になってしまいます。元はと言えば線なのですから、面積が無いのは当然なのです。しかし、面積が0でも、何も残らないわけではありません。そこには、長さ無限大の曲線からなるフラクタル図形がちゃんと現れるのです。

バリエーション

フィボナッチ文字列フラクタルは、描画のルールやパラメータを少し変更すると、いろいろなバリエーションが得られます。

0と1の入れ替え

まずは、0と1の入れ替えです。フィボナッチ文字列の0と1を全て逆にした上で、これまでと同じルールを適用してみると、図8の右のような結果になります。遠目で見るといずれも同じような模様になっていますが、0と1を入れ替えたものは全体が45度傾いています。また、細部をよく見ると曲線の曲がり方が異なっていますね。

図8-通常の曲線（左）と0と1を入れ替えた場合の曲線（右）。いずれもn = 17

異なる描画ルール

フィボナッチ文字列フラクタルの描画ルールは、表1で示した通りでしたが、これを表3のように変更してみます。

表3-新たな描画ルール
S_nのk文字目	S_nのk - 1文字目	動作
問わない	0	現在の向きに1単位前進し、	直前と同じ方向に90度向きを変える。
問わない	1	現在の向きに1単位前進し、	直前と逆の方向に90度向きを変える。

0と1のいずれの場合も直進して向きを変えますが、1に出会った場合だけ、次回から曲がる方向を左右逆にするというルールです。このルールで描いてみると、図9の左のようになります。右は、0と1を入れ替えてこのルールを適用した場合です。遠目で見るとやはりこれも同じ模様ですが、曲線の曲がり方が先ほどとはまた異なったものになっています。このルールでは、毎回必ず曲がるため、角と角の間の距離は全て同じになっています。

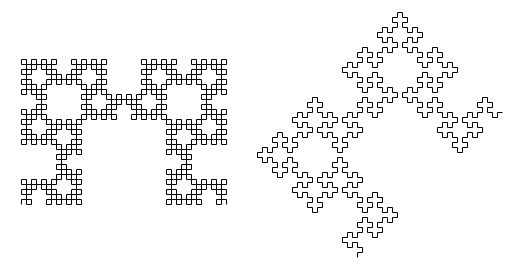
通常の曲線（左）と0と1を入れ替えた場合の曲線（右）。いずれもn = 17
図9-新たな描画ルールによる曲線（左）とさらに0と1を入れ替えた場合の曲線（右）。左はn = 16、右はn = 15

ここでは紹介しませんが、他にも様々な描画ルールが考案されています。

曲がる角度の変更

今までは、向きを変えるときは全て90度でしたが、この角度を変更してみましょう。図10は、曲がる角度を90度から、85度、80度、72度、60度に変更した場合です。60度の場合は、コッホ雪片の一部のようにも見えますね。なお、90度以上曲がった場合は、線が重なってしまい、見栄えの良いものは得られませんでした。

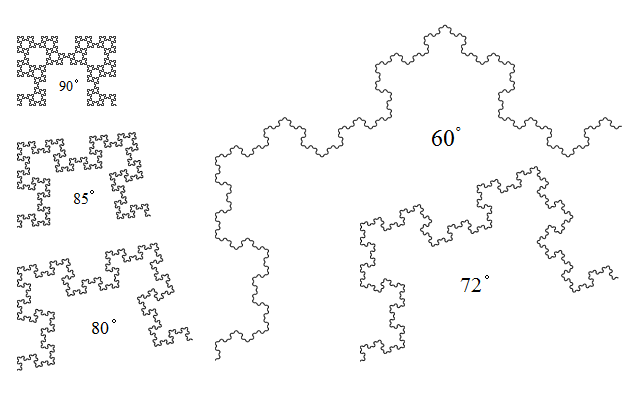
図10-曲がる角度を変更した場合の曲線

正方形の穴の大きさの変更

図11の左は、正方形に穴をあけていって、フィボナッチ文字列フラクタルのような図形に仕立てたものです。これまで見たＳ字型・Ｌ字型・コの字型を適当につなぎ合わせて、全体が正方形的な対称性を持つよう並べたものと見なせます。右側は、正方形の穴の大きさを、1 / √{2}倍にしたものです。こちらはもはやフィボナッチ文字列フラクタルではありませんが、相変わらずフラクタル的な美しい造形をしています。シェルピンスキーのカーペットに似ていますね。

図11-正方形型に仕立てたもの（左）と穴のサイズを変更したもの（右）