マンデルブロ集合を変化させる
マンデルブロ集合の楽しみ方は、拡大するだけではありません。パラメータを変更することで、異なった姿のマンデルブロ集合を描くことができます。
指数を変更する
マンデルブロ集合の定義を思い出してみましょう。
f(z) = z^2 + Cという関数を、z_0 = 0から始めて、
z_1 = f(z_0), z_2 = f(z_1), z_3 = f(z_2), …
とくり返し計算して数列を作っていったときに、k → ∞で|z_k|が発散しない複素数Cの集合
この二次関数f(z) = z^2 + Cがマンデルブロ集合の特徴的な形を生み出しているもとですが、この部分に別の関数を考えることもできます。まずは簡単に、指数を増加させたf(z) = z^n + C (n = 3,4,5,…)を考えてみましょう。

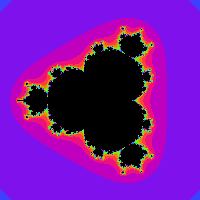

図4-1:指数を3(左)、4(中央)、5(右)にして描いたマンデルブロ集合
このように、マンデルブロ集合のこぶの数がどんどん増えていきます。こぶの数は指数nに対してn-1個になり、n-1回対称性(1/(n-1)回転すると同じになる)を持っています。こぶが増えるのは全体像だけではなく、細部を拡大したときに現れる分身も全て同様にこぶの数が増えているのが分かります。これらは、マルチブロット(Multibrot set)などと呼ばれることがあります。本来のマンデルブロ集合と同様にフラクタル図形となっており、拡大して楽しむことができます。
では、指数が2.5とか、非整数だったらどうなるでしょう。こぶが1つとこぶが2つの中間はどうなるのでしょうか?nを1から6まで連続的に変化させたときのマンデルブロ集合の形の変化をアニメーションにしました。ご覧下さい。
左側からどんどんこぶが生まれてきて、まるで生きているようですね。このように非整数の場合は、こぶが生まれる途中のような形になります。もちろん、これらを拡大したときに見られる分身も全て、そのような非常に中途半端な形をしています。また、整数の場合とは異なり、ところどころ集合が分裂しているような箇所も見受けられます。
ところで、指数が非整数の場合、累乗の計算は複素数の極形式で計算するしかありません。複素数の極形式とは、次のようなものです。
z = a + biのとき、|z| = (a^2 + b^2)^{1/2}, θ = tan^{-1}(b / a)とすると、
z = |z|(cosθ + i⋅sinθ) = |z|e^{θi}
極形式を使うと、累乗は指数が整数でなくても、次のように簡単に計算できます。
z^n = |z|^n(cosnθ + i⋅sinnθ) = |z|^ne^{nθi}
この中で、偏角θは、一般的には0 ≤ θ < 2πや-π < θ ≤ πの範囲で取りますが、非整数指数のマンデルブロ集合を描く場合は、偏角の範囲の取り方によって、こぶが生まれる様子に変化が現れます。先に示したアニメーションは、偏角を-π < θ ≤ πに取った場合のアニメーションです。改めて見ると、偏角が不連続となる実軸の負の方向に裂け目ができて、そこから偏角が0、すなわち実軸の正の方向に向かって湧き出るようにこぶが生まれているのが分かります。これ以外の偏角の取り方をした場合、同様に、偏角が不連続となる方向に裂け目ができて、そこから偏角が0の方向へ湧き出るようにこぶが生まれてきます。したがって、-π < θ ≤ πとした場合が、きれいに上下対称になるので、マルチブロットを描いたアニメーションの多くは偏角を-π < θ ≤ πで計算しています。
負の指数
では、nを負の数にした場合どうでしょう。nを0, -1, -2, …と小さくしていくことを考えます。nが負になった場合、数学的な意義はこれまでと変わってきてしまい、先に説明したような「|z_k| > 2となれば発散する」といった判定方法も使えなくなります。また、z = 0の場合、負の数nに対する0^nはゼロ除算となりますので、計算できなくなってしまいます。
このように負の指数の場合、本来のマンデルブロ集合とはだいぶ事情が異なってきてしまいますが、強引に今までのアルゴリズムを適用して描画してみると、以下のようになります。
指数が1以上の場合とは、全く異なった形が現れます。マンデルブロ集合はドーナツ状に外側に向かって広がり、その内側に複雑な模様が出てきます。これはこれでまた非常に不思議な造形を楽しむことができますが、実際に負の指数に対してより意味のあるマンデルブロ集合を考えるには別のアルゴリズムが必要になります。
初期座標による変化
次は、指数ではなくて、数列の初項z_0を変化させた場合です。f(z) = z^2 + Cの場合、z_0を0以外にすると数学的意義が薄れてしまいますが、数式上は実数に限らず複素数なら何でも取ることが可能で、それによる変化を楽しむことができます。全てを試すことはできませんので、ここでは実軸上と虚軸上の値をとった場合をアニメーションにしてみました。こんな風に変化します。
マンデルブロ集合が、溶けるようように小さくなって画面の外へ消えていってしまいます。z_0が0(原点)から離れていると、その分発散が速くなってしまう点が増えるため、集合の大きさが小さくなっていってしまうのでしょう。
